Electrical potential of the sphere

[Ivan Antunovic]

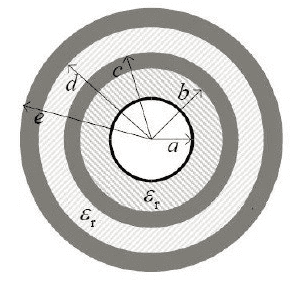
Metal ball ( Figure 5) radius a = 5 cm , is surrounded by two concentric metal shell of radius b = 10 cm and c = 15 cm , and d = 20 cm and e = 25 cm . The relative permeability of the dielectric between the ball and the first shell , and between the two shells is εr is 4. Outside the outer cross air . The charge of possession Q1 = 1 nC , a charge the outer shell is Q3 = -1 nC . What is the charge on the inner shell ( Q2 ) when the potential of the sphere and the outer shell ( in relation to the reference point at infinity ) are equal ( V1 = V3 )

{image inserted by moderator}

Homework Equations

The Attempt at a Solution

Tried to do this twice but I am getting the wrong result,it is supposed to be -7nC and I am getting 5nC, I can't see what am I doing wrong.

 

[Simon Bridge]

Please explain your reasoning.

 

[Ivan Antunovic]

Please explain your reasoning.

What do you mean?
I integrated from inifinity to e to find the potential V3 and from infinity-->e---->d----->c---->b---->a to get potential V1 and made V1=V3 ,I don't see any other way of doing this, only if something is wrong with my equations?

 

[gracy]

and between the two shells is εr is 4. Outside the outer cross air .

What do you mean? Isn't something wrong here?

 

[Simon Bridge]

I cannot easily follow your equations because you have not written any reasoning down.
If I do not know how you are thinking I don't know how to reply to you.

It looks like you found out the amount of work to assemble a sphere of known charge at the outer radius, then found the work to assemble a sphere charge Q at the ball radius, then found out the value of Q that makes these two figures the same. Something like that? Walk me through the physics you are using.
Note: I don't see a Q1 or a Q3 on your diagram.

 

[haruspex]

What do you mean?
I integrated from inifinity to e to find the potential V3 and from infinity-->e---->d----->c---->b---->a to get potential V1 and made V1=V3 ,I don't see any other way of doing this, only if something is wrong with my equations?

Unless the images are very clear and your handwriting impeccable, no corrections, it is quite hard to read working posted as images. Your attachments don't reach those high standards. Even then, it is hard to comment on such working unless you populate it liberally with reference numbers on the equations. The ability to post images on these forums is really just for diagrams and printed matter.

Even then, I cannot follow your working because you do not define the variables you introduce, like V₂ and V_dc.

 

[Ivan Antunovic]

Okay guys it's solved,sorry for the bad handwriting I don't know how to post it other way because I don't know how to use latex, and I've made mistake with '-' sign in my equations that was the reason for wrong result.I got Q2=-7nC now.

Note: I don't see a Q1 or a Q3 on your diagram.

Q1 was the charge on the inner ball, Q2 on the inner shell , and Q3 on the outter shell.

 

[haruspex]

Okay guys it's solved,sorry for the bad handwriting I don't know how to post it other way because I don't know how to use latex,

Latex is not essential. You can use the X₂, X² and ∑ buttons to make quite readable equations.

 

[gracy]

Is it spherical capacitor?

 

[SammyS]

Okay guys it's solved,sorry for the bad handwriting I don't know how to post it other way because I don't know how to use latex, and I've made mistake with '-' sign in my equations that was the reason for wrong result.I got Q2=-7nC now.

I don't get that answer.

 

[gracy]

is supposed to be -7nC

I got the answer to be -6nC.

Okay guys it's solved

As you are not posting how you solved that. You have solved this question on your own.
I don't think OP needs any further guidance , he is apparently finished with this thread. This type of unsolved threads annoy me personally and I think this is the case with most of the students .
(I hope I am not sounding like a mentor actually the reason behind this confidence is I have taken mentor's permission )

$V_1$ = $V_3$$V_1$=$\frac{KQ1}{a}$ + $\frac{KQ2}{c}$ +$\frac{KQ3}{e}$ = $V_3$ =$\frac{K}{R}$ ($Q_1$+$Q_2$ +$Q_3$)Put values given[ K=4 everywhere (given)]$V_3$= $\frac{4}{25 × 10^-2}$ $Q_2$ (as $Q_1$ +$Q_3$ came out to be zero) = 16$Q_2$$V_1$=$4$ (20 + $\frac{20Q_2}{3}$ -4) =$4$( $\frac{60+20Q_2-12}{3})$16$Q_2$ =$4$ ($\frac{60+20Q_2-12}{3})$ 4$Q_2$=$\frac{48+20Q_2}{3}$12$Q_2$=48 + $20Q_2$-8 $Q_2$=48$Q_2$=-6 nC

 

[Ivan Antunovic]

I got the answer to be -6nC.

As you are not posting how you solved that. You have solved this question on your own.
I don't think OP needs any further guidance , he is apparently finished with this thread. This type of unsolved threads annoy me personally and I think this is the case with most of the students .
(I hope I am not sounding like a mentor actually the reason behind this confidence is I have taken mentor's permission )

$V_1$ = $V_3$$V_1$=$\frac{KQ1}{a}$ + $\frac{KQ2}{c}$ +$\frac{KQ3}{e}$ = $V_3$ =$\frac{K}{R}$ ($Q_1$+$Q_2$ +$Q_3$)Put values given[ K=4 everywhere (given)]$V_3$= $\frac{4}{25 × 10^-2}$ $Q_2$ (as $Q_1$ +$Q_3$ came out to be zero) = 16$Q_2$$V_1$=$4$ (20 + $\frac{20Q_2}{3}$ -4) =$4$( $\frac{60+20Q_2-12}{3})$16$Q_2$ =$4$ ($\frac{60+20Q_2-12}{3})$ 4$Q_2$=$\frac{48+20Q_2}{3}$12$Q_2$=48 + $20Q_2$-8 $Q_2$=48$Q_2$=-6 nC

I used formula for electrical potential ,-integral of E*dl integrating from reference point to point r(for V3 r=e)
Integrating from infinity to e gives ,where by gauss law in the vacuum using only epsilon zero in k ,E = k*(Q1+Q2+Q3)/r^2 , I get V3=k*(Q1+Q2+Q3)/e,

now integrating(V) from point e to point d ( there is no E field in the metal so Ved = 0), integrating from d to c where there is some insulator with epsilon=4*epsilon0 I get by gauss law E= (Q1+Q2) /4pi*epsilon*r^2 ,and V2= V1 + ((Q1+Q2) /4pi*epsilon ) * (d-c/c*d).

Gauss law going from c--->d ,no charge ,no E field.

at b>r>a , Q=Q1 , so by gauss law I get that E = Q1/4*pi*epsilon * r^2 , and using integral for V from b to a ,I get V1 = ( V2 + Q1/4*pi*epsilon )*(b-a/a*b)

since V3=V1

V3 = V3 + ( Q1+Q2/4*pi*epsilon)*(d-c/c*d)+(Q1/4*pi*epsilon)*(b-a/a*b)

Put all the unknowns in and you get

Q2= - 7nAs

This solution was posted in my pictures.I just messed up with signs somewhere , maybe I didn't made myself clear enough , that was the reason I wasn't posting the same solution , but I had to now.

 

[Ivan Antunovic]

Delete this post, I double posted by accident.

 

[TSny]

$V_1$=$\frac{KQ1}{a}$ + $\frac{KQ2}{c}$ +$\frac{KQ3}{e}$ = $V_3$ =$\frac{K}{R}$ ($Q_1$+$Q_2$ +$Q_3$)

These expressions for V₁ and V₃ are not correct. The dielectric constant K should appear in the denominator, not the numerator. You also need to include Coulomb’s constant k that would appear in the numerator (or, equivalently $4 \pi \epsilon_0$ in the denominator).

To get a correct expression for V₃, start at infinity where V = 0 and think about the change in potential as you move from infinity to the surface of the outer conductor (r = e). In the region of space where r > e, there is no dielectric material. So, the dielectric constant K is equal to 1 in this region.

But you actually don’t need to worry about getting an expression for the potential V₃. We just want to make sure that V₁ = V₃. In other words, we require the change in potential ΔV _{d→ a} to equal zero as we go from a point on the outer shell to a point on the sphere. Note that

ΔV _{d→ a} = ΔV _{d→ c} + ΔV _{c→ b} + ΔV _{b→ a}.

Each of these terms can be worked out without having to know the potential V₃ or V₁

This is what Ivan did in post #12.

 

[gracy]

These expressions for V1 and V3 are not correct. The dielectric constant K should appear in the denominator, not the numerator. You also need to include Coulomb’s constant k that would appear in the numerator.

After correcting these mistakes am I supposed to get the right answer? Or my complete method is wrong?

 

[TSny]

You should get the correct expression for V₃ with these corrections. However, I think your expression for V₁ will need more work. The only way that I can see to get V₁ is to start with V₃ and then add the additional change in V as you go from the outer shell to the sphere.

But if you can get an expression for ΔV as you go from d to a, then you can solve the problem by just setting ΔV_{d→ a} = 0. You won't need to know V₃ or V₁.

 

[gracy]

expression for V1 will need more work.

Why? Why $V_1$≠$\frac{KQ1}{ka}$ +$\frac{KQ2}{kc}$ + $\frac{KQ3}{ke}$ Here k is dielectric constant and K is coulomb constant.

 

[TSny]

You still don't have the k and the K in the right place. I'm assuming k is Coulomb's constant and K is the dielectric constant.

But, even if you fix that, your expression for V₁ is not correct. What is your reasoning for writing that expression? I don't understand what each of the three terms represents.

 

[gracy]

You still don't have the k and the K in the right place

I think it is correct. It's just that I took k = dielectric constant and K =coulomb constant.

The dielectric constant K should appear in the denominator

Here k is dielectric constant

Coulomb’s constant k that would appear in the numerator

K is coulomb constant.

 

[gracy]

But, even if you fix that, your expression for V1 is not correct. What is your reasoning for writing that expression? I don't understand what each of the three terms represents.

$V_1$ = Potential of sphere (having radius a)

= potential due to charge on itself + potential due to charge on sphere having radius c + potential due to charge on sphere having radius e

=$\frac{KQ1}{ka}$ + $\frac{KQ2}{kc}$ +$\frac{KQ3}{ke}$

 

[TSny]

$V_1$ = Potential of sphere (having radius a)

= potential due to charge on itself + potential due to charge on sphere having radius c + potential due to charge on sphere having radius e

=$\frac{KQ1}{ka}$ + $\frac{KQ2}{kc}$ +$\frac{KQ3}{ke}$

This is not correct. For example, I believe the potential at the sphere due to just Q₂ works out to be $V = \frac{Q_2}{4 \pi \epsilon_0} \left( \frac{1}{e} + \frac{1}{Kc} - \frac{1}{Kd} \right)$, where K is the dielectric constant (K = 4). To find this, you need to consider the electric field produced by Q₂ alone and then consider the potential produced by this field.

Likewise, you can work out the potential at the sphere due to just Q₁ or just Q₃.

But, I think it's much easier to solve the problem by determining the net electric field with all the charge in place and then consider the potential difference between the outer shell and the sphere using this net field. This is Ivan's method.