jhonnyS
- 2
- 0
- TL;DR
- what is the real time process for the wave function when an electron is living in a potential well, and an other is aproaching?
For example, we have this two potencial wells approaching, the electron is confined in one.
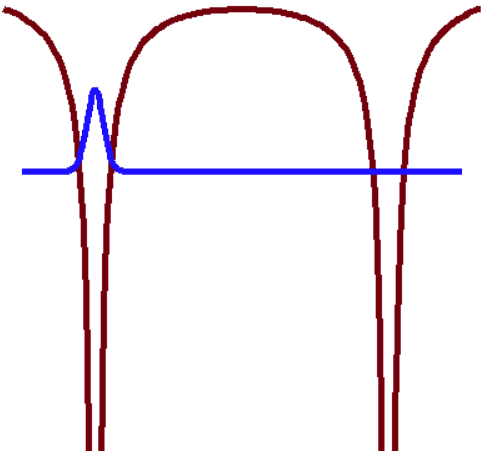
the final appearance will be like this:
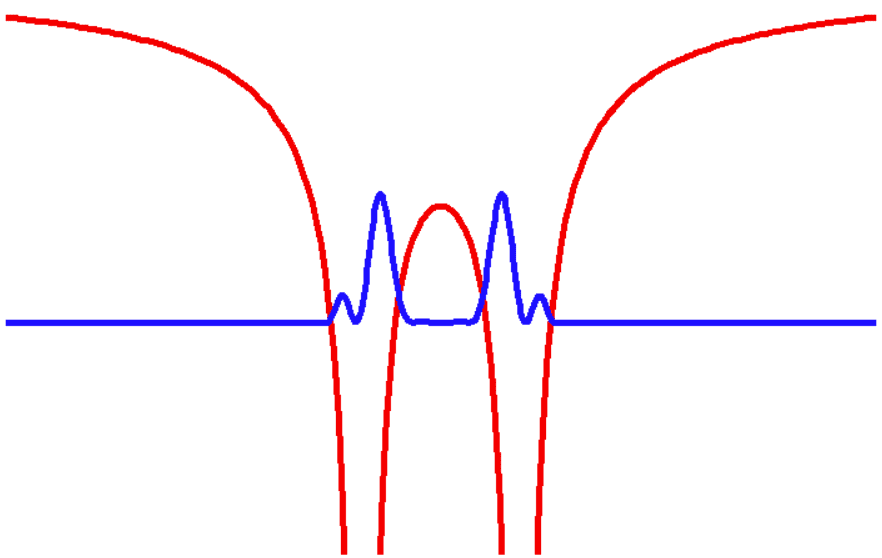
THEN, if we know a wave packet is formed by many frequencies, but in a potencial well there are just few frequencies allowed, energy levels, so let's say, one frequency adapted to... the form of the potential.
In the point when the electron begins to overstep to the other potential, and the wave "don't know there is a well that will confine it later" so cannot mantain this unic frequency component because there were the posibility to extend indefinitely. NEEDs more frequencies to form a "wave packet" to contain itself BUT this frequencies, at same time, are not allowed for the part of wave function that remains confined in the initial potential well.
thank you
the final appearance will be like this:
THEN, if we know a wave packet is formed by many frequencies, but in a potencial well there are just few frequencies allowed, energy levels, so let's say, one frequency adapted to... the form of the potential.
In the point when the electron begins to overstep to the other potential, and the wave "don't know there is a well that will confine it later" so cannot mantain this unic frequency component because there were the posibility to extend indefinitely. NEEDs more frequencies to form a "wave packet" to contain itself BUT this frequencies, at same time, are not allowed for the part of wave function that remains confined in the initial potential well.
thank you