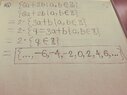Math100
- 817
- 230
- Homework Statement
- Write each of the following sets by listing their elements between braces.
- Relevant Equations
- None.
I've boxed around my answer but I don't know if this is the right answer. I also used a substitution with c=3a+b in my work. I don't know if my work is precise or not.