Solve these simultaneous equations that involve vectors

[chwala]

Homework Statement

See attached

Relevant Equations

understanding of vectors and simultaneous equation

Find the question and solution here;

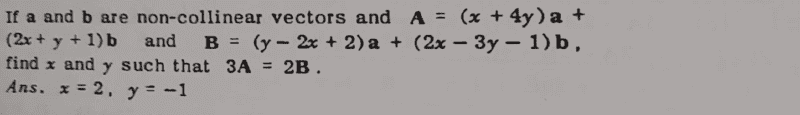Ok, i was able to solve this by using,
$3A=3ax+12ay+6bx+3by+3b$
$2B=2ay-4ax+4a+4bx-6by-2b$

leading us to the simultaneous equation;
$7x+10y=4$
$2x+9b=-5$
$x=2$ and $y=-1$

I had initially tried the approach of using $3A=2B$ →$B=1.5A$ ...Then on substituting this in $A$, I got
$B_1= 1.5a(x+4y) + 1.5b(2x+y+1)$ this ought to be equal to,
$B_2 = a(y-2x+2)+b(2x-3y-1)$

giving me the simultaneous equation,
$3.5x+5y=2$
$x+4.5b=-2.5$

aaaaargh this is also correct, i had missed out on a term...

any other approach guys welcome...

 

[FactChecker]

I had initially tried the approach of using $3A=2B$ →$B_1=1.5A$ ...Then on substituting this in $A$, I got
$B_1= 1.5a(x+4y) + 1.5b(2x+y+1)$ this ought to be equal to,

This looks wrong. I don't understand what you did here.
If you are trying to figure out alternative methods to simultaneous equations, why? IMHO, if you really understood simultaneous equations, you would not be looking for something else.

 

[chwala]

This looks wrong. I don't understand what you did here.
If you are trying to figure out alternative methods to simultaneous equations, why? IMHO, if you really understood simultaneous equations, you would not be looking for something else.

I think both simultaneous equations are correct...I will check and confirm later...I was thinking of a possibility of a much faster approach but I guess it doesn't matter. Cheers man.

Note;
I just amended a term in the second simultaneous equation.
Take note that in the second simultaneous equation, i was equating $B$=$B$ ...

 

[PeroK]

I think both simultaneous equations are correct...I will check and confirm later...I was thinking of a possibility of a much faster approach but I guess it doesn't matter. Cheers man.

Note;
I just amended a term in the second simultaneous equation.
Take note that in the second simultaneous equation, i was equating $B$=$B$ ...

Note that $\mathbf a$ and $\mathbf b$ are vectors. Something like:

$2x+9b=-5b$

Cannot be right, as $x$ is a number.

The key to the problem is that two non-colinear vectors are linearly independent.

 

[chwala]

Note that $\mathbf a$ and $\mathbf b$ are vectors. Something like:Cannot be right, as $x$ is a number.

The key to the problem is that two non-colinear vectors are linearly independent.

Sorry a typo, let me amend it...the vectors are $a$ and $b$ ...$x$ and $y$ are scalar quantities.

 

[PeroK]

Sorry a typo, let me amend it...the vectors are $a$ and $b$ ...$x$ and $y$ are scalar quantities.

Okay, I see what you've done now. Writing $b$ instead of $\mathbf b$ and then mistyping $b$ instead of $y$ and $-5b$ instead of $-5$ was too many errors for me to follow what you were doing.

 

[chwala]

Okay, I see what you've done now. Writing $b$ instead of $\mathbf b$ and then mistyping $b$ instead of $y$ and $-5b$ instead of $-5$ was too many errors for me to follow what you were doing.

My silly me...Will try to go a bit slower in my typing...