guyvsdcsniper
- 264
- 37
- Homework Statement
- On a horizontal table, there lies a very long straight wire (current I), and a square conduct-ing loop (side L). The loop is oriented at 45 degrees, with its closest corner a
distance L/2 from the wire. If the loop is pulleddirectly away from the wire with constant speed v,
what emf is generated?
- Relevant Equations
- Emf
Setting up the integral to find the flux that is giving me trouble.
I know that I will have to break up this integral into 2 parts, the first part account for when the start of the loop is increasing in area, and another right when I pass the halfway mark of the loop and the area begins to decrease again.
I have denoted the area as wds, where w is the the width and ds is it the infinitesimal distance from the wire.
I believe it is a correct approach to have w for the lower half of the loop to be ##(s-\frac{L}{2})##
I was told by a friend I should multiply w by 2 to account for both halves of the loop.
Where I feel uneasy is my w for the area of the loop decreasing in size. I have it as ##(s+\frac{L}{2})##. Does this choice make sense?
I also feel uneasy about picking my bounds. I know for sure that my first integral will start at L/2. Would the upper bound be ##2\sqrt(L)##?
My friend told me the first upper limit should be ##2\frac{\sqrt(L)}{2}##.
I would appreciate any help I can get with this problem.
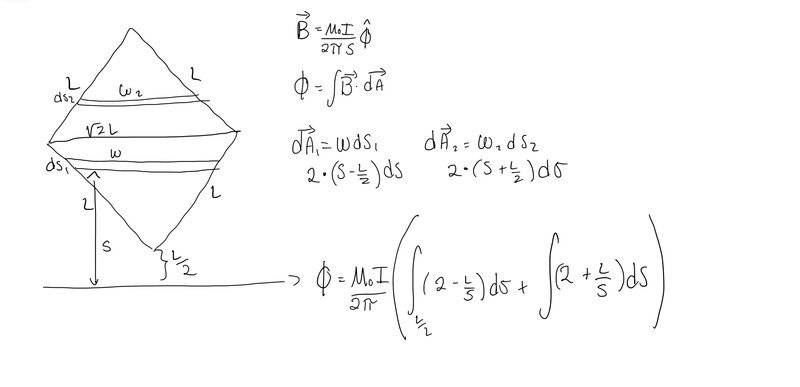
I know that I will have to break up this integral into 2 parts, the first part account for when the start of the loop is increasing in area, and another right when I pass the halfway mark of the loop and the area begins to decrease again.
I have denoted the area as wds, where w is the the width and ds is it the infinitesimal distance from the wire.
I believe it is a correct approach to have w for the lower half of the loop to be ##(s-\frac{L}{2})##
I was told by a friend I should multiply w by 2 to account for both halves of the loop.
Where I feel uneasy is my w for the area of the loop decreasing in size. I have it as ##(s+\frac{L}{2})##. Does this choice make sense?
I also feel uneasy about picking my bounds. I know for sure that my first integral will start at L/2. Would the upper bound be ##2\sqrt(L)##?
My friend told me the first upper limit should be ##2\frac{\sqrt(L)}{2}##.
I would appreciate any help I can get with this problem.