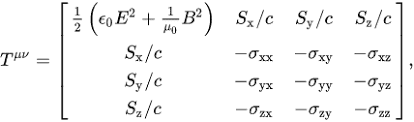SUMMARY
The energy-stress tensor in General Relativity (GR) incorporates all forms of stress-energy, including contributions from electromagnetic fields and matter. It is not limited to electromagnetic energy density, as it also accounts for mechanical aspects of charges and stress-energy from various sources. The most general form of the stress-energy tensor is given by the equation Tμν = ± (2/√|g|) δS/δgμν, where S is the action relevant to the system. Understanding the complete nature of the stress-energy tensor is crucial for accurate modeling in GR.
PREREQUISITES
- Understanding of General Relativity (GR) principles
- Familiarity with the stress-energy tensor and its components
- Knowledge of electromagnetic field theory
- Basic concepts of fluid dynamics in relativistic contexts
NEXT STEPS
- Study the derivation and applications of the stress-energy tensor in General Relativity
- Explore the role of the electromagnetic field in the energy-momentum tensor
- Investigate the ideal fluid model and its implications for stress-energy calculations
- Learn about the Einstein-Hilbert action and its relationship to the stress-energy tensor
USEFUL FOR
Physicists, particularly those specializing in General Relativity, theoretical physicists, and researchers in high-energy physics will benefit from this discussion.