Equation of line bisecting two others

[ps098]

Hi everyone, this will probably be very easy for someone but I'm really struggling to get this to work. I have experimental data whose baseline and peak midpoints I have fitted tangents to, and I have found the points where they intersect. I now want to find the red line which bisects these two tangents, but whatever I do the plot comes out at completely the wrong angle. I have included an example, with my beautiful handwritten workings (lol).

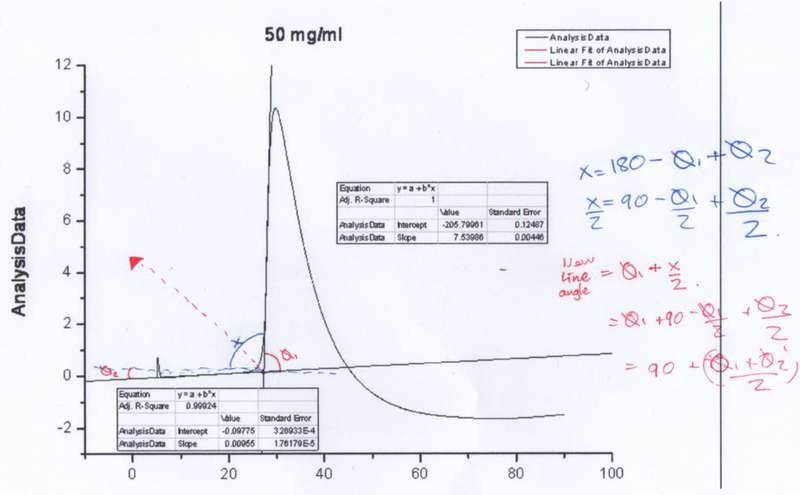
If anyone can help, I'd really appreaciate it, my MSc will be all the better for it :D

Cheers

 

[pmsrw3]

Well. Let's say your first line has slope m1, and your second m2 (both positive in the example graph). A line with slope m1 is slanted at angle arctan(m1) to the horizontal. You, however, want to think of this first line as heading down and left, so you should add pi radians or 180 degrees to it. Your two lines, then, are at angles

$$\begin{eqnarray*}<br /> \theta_1 & = & \arctan{(m_1)}+180 \\<br /> \theta_2 & = & \arctan{(m_2)}<br /> \end{eqnarray*}$$

The line you wants heads at an angle halfway inbetween

$$\theta_b = \frac{\theta_1+\theta_2}{2}$$

and its slope is $m_b=\tan(\theta_b)$, which will be negative. Find a line with that slope that goes through the intersection point.

 

[ps098]

Thanks ever so much for that, I've been staring at the thing for literally hours trying to figure out what was wrong with my equation - always good to get a fresh brain on the problem!

One thing I can't figure out, will this formula still apply if the baseline is at a negative slope?

 

[pmsrw3]

One thing I can't figure out, will this formula still apply if the baseline is at a negative slope?

As long as your arctan function returns a negative angle for a negative argument (and I've never met one that doesn't), it should work. I guess you could in theory run into a problem in which the bisecting line is vertical and has infinite slope. That would take very bad luck.

Another possibility, which I just advised someone else to try, would to be use the two-argument form of the arc tangent function, $\theta_1=\arctan(-1,-m_1)$. Then you don't have to add 180.