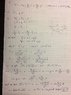Discussion Overview
The discussion revolves around the stability of electric charge equilibrium as described by the equation x^2+3x-0.45=0, which yields two solutions for charge positions. Participants explore the use of derivatives to determine stability and the conditions under which a test charge is in equilibrium with two other charges, including considerations of force and field directions.
Discussion Character
- Homework-related
- Mathematical reasoning
- Debate/contested
Main Points Raised
- Some participants suggest using the first derivative to assess stability at the equilibrium points x1=0.14 and x2=-3.14.
- Others question whether the reasoning about stability based on the first derivative is correct, particularly in the context of the forces acting on the test charge.
- One participant expresses uncertainty about the charge's location and stability, suggesting that the charge should be on the x-axis between two other charges.
- Another participant emphasizes the need for the net forces to cancel out for equilibrium, raising concerns about the conditions under which this occurs.
- There is a discussion about the nature of the test charge, with some participants clarifying its charge and position relative to other charges.
- Graphical representations of the force field and net force equations are requested to better understand the situation.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the stability of the charge at the equilibrium points, with multiple competing views regarding the application of derivatives and the conditions for equilibrium. The discussion remains unresolved regarding the correct interpretation of the forces involved.
Contextual Notes
Participants express uncertainty about the assumptions made regarding the charge placements and the implications of the mathematical results. There are also unresolved questions about the graphical representation of the force field and net forces.