Maggie_s2020
- 2
- 0
Hello, I have been trying to solve the top line equation to get the result (the bottom line). I am searching for a clue (the steps) on how to obtain those four brackets as a result.
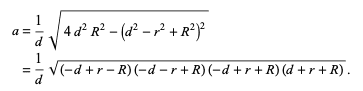
Last edited by a moderator: