Problems with the interpretation of the Torsion tensor and the Lie Bracket

[PhysicsObsessed]

Hi,
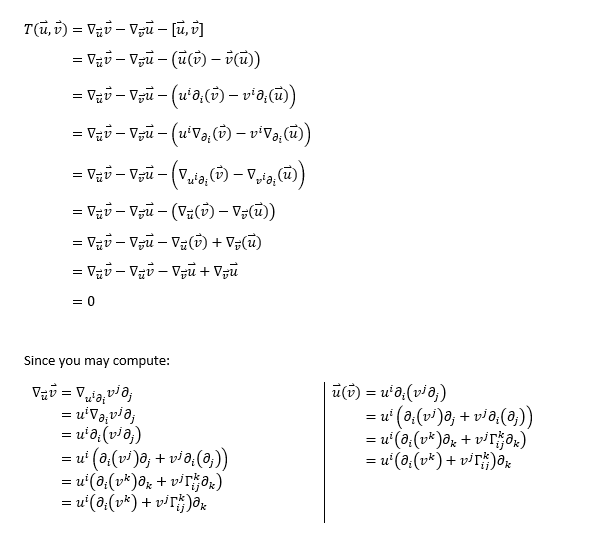
I've been doing a course on Tensor calculus by Eigenchris and I've come across this problem where depending on the way I compute/expand the Lie bracket the Torsion tensor always goes to zero. If you have any suggestions please reply, I've had this problem for months and I'm desperate to solve it.

I tried computing an actual example on a spherical manifold with some simple vector fields u and v to see if that would help clarify the issue, however it didn't turn out. Though I believe the problem lies with the u(v) being equal to ∇_u(v), which shouldn't be the case.

I screenshotted the problem below, but I'll add some clarification on the notation here:

• vector / vector field: any letter with a harpoon on top
• partial derivative operator (w respect to coordinate variables): del
• covariant derivative: nabla symbol
• connection coefficients / Christoffel symbols: capital gamma
• contravariant component: the index will be a superscript (see the vector field components u^i)
• covariant component: the index will be a subscript (see the basis vectors / partial derivatives del_i)
• Torsion tensor: T (capital T)
• Lie bracket: [] (square brackets)
• Also, I'm using index notation / Einstein notation to represent summations

 

[jedishrfu]

Can you show us your work and use Latex to do it?

There is a reference page on PF with Latex formatting guidelines.

https://www.physicsforums.com/help/latexhelp/

 

[PhysicsObsessed]

Can you show us your work and use Latex to do it?

There is a reference page on PF with Latex formatting guidelines.

https://www.physicsforums.com/help/latexhelp/

Alright, yeah, I've never used Latex before so it might take a while but I'll give it a go, you mean the example calculation right? Thanks for the link btw.

 

[martinbn]

Though I believe the problem lies with the u(v) being equal to ∇_u(v), which shouldn't be the case.

$u(v)$ is not $\nabla_u(v)$. Assuming it implies the torsion is zero. In fact it is stronger than that. Torsion zero is equivalent to $u(v)-v(u)=\nabla_u(v)-\nabla_v(u)$.

$u(v)$ is not a vector field, it is a second order operator.

 

[PhysicsObsessed]

$u(v)$ is not $\nabla_u(v)$. Assuming it implies the torsion is zero. In fact it is stronger than that. Torsion zero is equivalent to $u(v)-v(u)=\nabla_u(v)-\nabla_v(u)$.

$u(v)$ is not a vector field, it is a second order operator.

Hi, thanks a lot,
I thought the error might be there, although I'm really new to this area could you explain what you mean by a second order operator? Do you mean something like $\frac{\partial^2}{\partial x^i\partial x^j}$?

 

[martinbn]

Do you mean something like $\frac{\partial^2}{\partial x^i\partial x^j}$?

Yes. And the reason that the Lie bracket is a vector field is because all the mixed second derivatives are equal and will cancel.

 

[strangerep]

• connection coefficients / Christoffel symbols: capital gamma

Christoffel symbols are symmetric in their lower indices, hence their torsion is always zero.

 

[PhysicsObsessed]

Christoffel symbols are symmetric in their lower indices, hence their torsion is always zero.

Hi, thanks for the help; though I was under the impression that this only applied in some cases, like for the connection coefficients of the Levi-Civita connection, but not in every case.

 

[martinbn]

Christoffel symbols are symmetric in their lower indices, hence their torsion is always zero.

You reserve the name "Christoffel symbols" only for symmetric connections.

 

[strangerep]

[...] I was under the impression that this only applied in some cases, like for the connection coefficients of the Levi-Civita connection, but not in every case.

Yes, but you specified "Christoffel symbols" explicitly.

 

[martinbn]

Yes, but you specified "Christoffel symbols" explicitly.

Yes, but some use it for any connection.

 

[AboveSky]

You reserve the name "Christoffel symbols" only for symmetric connections.

I would even reserve this name for the specific connection implied by the metric.

 

[PhysicsObsessed]

Yes, but you specified "Christoffel symbols" explicitly.

I would even reserve this name for the specific connection implied by the metric.

Oh, I wasn't aware, thanks for the comment, I'll make sure to be more careful in the future. But yes the problem is meant to be for an arbitrary connection, not specifically for the Levi-Civita connection.

 

[lavinia]

Oh, I wasn't aware, thanks for the comment, I'll make sure to be more careful in the future. But yes the problem is meant to be for an arbitrary connection, not specifically for the Levi-Civita connection.

Hi, thanks for the help; though I was under the impression that this only applied in some cases, like for the connection coefficients of the Levi-Civita connection, but not in every case.

The terminology "Christoffel symbols" seems to specifically refer to a Levi-Civita connection so the Christoffel symbols are always symmetric. This may be because Christoffel first defined his symbols in terms of a Riemannian metric on a manifold. And he had no concept of a connection but rather was looking at transformations of differential expressions from one coordinate system to another.

For an arbitrary connection you are right. The coefficients with respect to a coordinate basis need not be symmetric. If they are symmetric in every coordinate system the connection is called symmetric but such a connection may not be a Levi-Civita connection.

 

[lavinia]

@PhysicsObsessed

I thought this might be helpful.

Given a vector field $U$ and a smooth function $f$ one can differentiate $f$ with respect to $U$ to get a new function $U⋅f$. At each point $p$, $U⋅f$ is the derivative of $f$ along a curve whose velocity vector at $p$ is $U_{p}$. Since $U⋅f$ is itself a smooth function, it can also be differentiated with respect to any other vector field $V$ to get a third function $V⋅(U⋅f)$.

Notice that no vector fields are being differentiated. There is no covariant derivative here, just ordinary derivatives of functions. This should alert you to the problem that you have been having with the computation in your opening post.

The Lie bracket acting on $f$ is just the difference of the two functions $U⋅(V⋅f)$ and $V⋅(U⋅f)$

$[U,V]⋅ f= (U⋅(V⋅f))-V⋅(U⋅f)$. It is a differential operator that acts on functions.

But there is more. Even though it uses double derivatives, it is only first order as @martinbn pointed out.

One can see this by writing out all of the derivatives in local coordinates or by appealing to the definition of a tangent vector at a point as a linear operator on functions (linear over the real numbers) that also satisfies the Leibniz rule.

The Leibniz rule(product rule) says that for functions $f$ and $g$, $U_{p}⋅fg = f(p)U_{p}⋅g + g(p)U_{p}⋅f$.

A smooth vector field(or just a vector field) is a smooth choice of a tangent vector at each point in a region of the manifold. For instance in a coordinate chart the operators $∂/∂x_{j}$ are vector fields.

For the Lie bracket, this operator definition can be checked purely formally without reference to coordinates.

The Lie bracket of two vector fields is only one example of a differential operator that is a tensor.
Take for instance the exterior derivative of a 1 form. The definition is

$dw(U_{p},V_{p})=U_{p}⋅w(V)-V_{p}⋅w(U)-w([U,V]_{p})$

This involves derivatives of $w(U)$ and $w(V)$ so its value at any point $p$ might depend on how $U{_p}$ and $V_{p}$ are extended to be vector fields. For $dw$ to be a tensor $dw(U_{p},V_{p})$ must be independent of the extensions.

Another example is the covariant derivative of a 1 form.

$(∇w)(U_{p},V_{p}) = U_{p}⋅w(V)-w(∇_{U_{p}}V)$

where $∇_{U_{p}}V$ is the covariant derivative of the vector field $V$ with respect to the tangent vector $U_{p}$. Like the exterior derivative of a 1 form, this is a $(0,2)$ tensor.

Symmetry and Torsion

Here is one way to see that a connection is symmetric if and only if the torsion tensor is identically zero.

The covariant derivative of a 1 form $∇w$ is symmetric if $∇w(U_{p},V_{p})=∇w(V_{p},U_{p})$ for every pair of vectors at every point $p$.

Subtracting and plugging in the definition of the covariant derivative gives

$0=∇w(U,V)-∇w(V,U)= U⋅w(V)-V⋅w(U) -w(∇_{U}V-∇_{V}U)$

and adding and subtracting $w([U,V])$ gives

$0 = (U⋅w(V)-V⋅w(U)-w([U,V])) -w(∇_{U}V-∇_{V}W-[U,V]) =$dw(U,V)-w(Tor(U,V))$at each point. If$w$is closed i.e.$dw=0$then$∇w$is symmetric if and only if$w$is identically zero on all values of the torsion tensor at every point. In any local coordinate system the coordinate 1 forms$dx_{j}$are closed and if their covariant derivatives are symmetric tensors (as in a Levi-Civita connection) then they must all be zero on the torsion tensor. Since they form a basis for the tangent spaces, the only way this can happen is if the torsion tensor is identically zero in the coordinate system. In a symmetric connection this holds in every coordinate system. Comment: The equation$∇w(U,V)-∇w(V,U)= U⋅w(V)-V⋅w(U) -w(∇_{U}V-∇_{V}U) $is always true for any 1 form. If one assumes that the torsion tensor is zero then the equation becomes$∇w(U,V)-∇w(V,U)= U⋅w(V)-V⋅w(U) -w([U,V]) = dw(U,V)##

This would give another definition of a symmetric connection.

 

[PhysicsObsessed]

Wow, this is a pretty spectacular post! I'm going to read it in a bit cause I currently have an assignment on, but thanks so much for putting the effort in to answer my question in such detail

 

[PhysicsObsessed]

Wow, this is a pretty spectacular post! I'm going to read it in a bit cause I currently have an assignment on, but thanks so much for putting the effort in to answer my question in such detail

Okay, I just read through the response, and I am happy to say, after like half a year, I finally know what was wrong XD