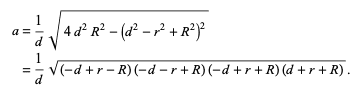Expanding and simplifying brackets

  • Context: MHB 
  • Thread starter Thread starter Maggie_s2020
  • Start date Start date
  • Tags Tags
    Expanding Simplifying
Click For Summary
SUMMARY

The discussion focuses on the algebraic manipulation of the expression $4d^2R^2 - (d^2 - r^2 + R^2)^2$ to achieve a simplified factored form. The steps outlined include recognizing the difference of squares and systematically applying factoring techniques to arrive at the final expression $(-d+r+R)(-d-r+R)(-d+r-R)(d+r+R)$. Key transformations involve breaking down the expression into manageable components and utilizing the properties of squares effectively.

PREREQUISITES
  • Understanding of algebraic expressions and factoring techniques
  • Familiarity with the difference of squares concept
  • Knowledge of polynomial manipulation
  • Basic skills in handling radical expressions
NEXT STEPS
  • Study advanced factoring techniques in algebra
  • Learn about polynomial identities and their applications
  • Explore the properties of radicals and their simplifications
  • Investigate the use of algebraic expressions in real-world problem solving
USEFUL FOR

Students, educators, and anyone interested in mastering algebraic manipulation and simplification techniques, particularly in the context of factoring complex expressions.

Maggie_s2020
Messages
2
Reaction score
0
Hello, I have been trying to solve the top line equation to get the result (the bottom line). I am searching for a clue (the steps) on how to obtain those four brackets as a result.
Screenshot 2020-12-06 at 16.41.07.png
 
Last edited by a moderator:
Mathematics news on Phys.org
factoring the expression within the radical just involves the difference of squares ...

$4d^2R^2 - (d^2-r^2+R^2)^2$

$(2dR)^2 - (d^2-r^2+R^2)^2$

$[2dR -(d^2-r^2+R^2)] \cdot [2dR + (d^2-r^2+R^2)]$

$[-(d^2-2dR+R^2) + r^2] \cdot [(d^2+2dR+R^2) - r^2]$

$[r^2-(d-R)^2] \cdot [(d+R)^2 - r^2]$

$[(r-d+R)(r+d-R)] \cdot [(d+R-r)(d+R+r)]$

multiply the two middle factors by (-1) ...

$(-d+r+R)(-d-r+R)(-d+r-R)(d+r+R)$
 
Last edited by a moderator:
skeeter said:
factoring the expression within the radical just involves the difference of squares ...

$4d^2R^2 - (d^2-r^2+R^2)$

$(2dR)^2 - (d^2-r^2+R^2)^2$

$[2dR -(d^2-r^2+R^2)] \cdot [2dR + (d^2-r^2+R^2)]$

$[-(d^2-2dR+R^2) + r^2] \cdot [(d^2+2dR+R^2) - r^2]$

$[r^2-(d-R)^2] \cdot [(d+R)^2 - r^2]$

$[(r-d+R)(r+d-R)] \cdot [(d+R-r)(d+R+r)]$

multiply the two middle factors by (-1) ...

$(-d+r+R)(-d-r+R)(-d+r-R)(d+r+R)$
THANK YOU SO SO SO MUCH! BLESS YOU!
 

Similar threads

MHB Expanding Brackets: Math Help for 2nd Term Maths
  • · Replies 4 ·
Replies
4
Views
2K
MHB Simplifying and expanding expressions
  • · Replies 5 ·
Replies
5
Views
2K
MHB Which simplifying method should be used to simplify 2x^2y^2 times 5xy^4?
  • · Replies 1 ·
Replies
1
Views
2K
High School Could someone verify how this simplifies?
  • · Replies 15 ·
Replies
15
Views
2K
High School Adding 'x' to 'xy' for Resultant <=1: A Table Guide
  • · Replies 18 ·
Replies
18
Views
2K
High School Need an on-line calculator for a simple calculation
  • · Replies 12 ·
Replies
12
Views
3K
MHB Rearranging Formulas: Finding W in Terms of M and L
  • · Replies 5 ·
Replies
5
Views
2K
High School What is the use of simplifying a question in math?
  • · Replies 3 ·
Replies
3
Views
1K
High School Missing out on intermediate algebraic steps
  • · Replies 23 ·
Replies
23
Views
2K
Graduate Problems with the interpretation of the Torsion tensor and the Lie Bracket
  • · Replies 16 ·
Replies
16
Views
6K