- #1
Nezva
- 46
- 0
I've never seen an expectation value taken and would greatly appreciate seeing a step by step of how it is done. Feel free to use any wavefunction, this is the one I've been trying to do:
In the case of [tex]\Psi=c[/tex]1[tex]\Psi[/tex]1[tex] + c[/tex]2[tex]\Psi[/tex]2[tex] + ... + c[/tex]n[tex]\Psi[/tex]n
And the operator A(hat) => A(hat)[tex]\Psi[/tex]1 = a1[tex]\Psi[/tex]1; A(hat)[tex]\Psi[/tex]2 = a2[tex]\Psi[/tex]2; A(hat)[tex]\Psi[/tex]n = an[tex]\Psi[/tex]n
Calculate: [tex]\left\langle\Psi\left|A(hat)\right|\right\Psi\rangle[/tex]
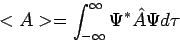
In the case of [tex]\Psi=c[/tex]1[tex]\Psi[/tex]1[tex] + c[/tex]2[tex]\Psi[/tex]2[tex] + ... + c[/tex]n[tex]\Psi[/tex]n
And the operator A(hat) => A(hat)[tex]\Psi[/tex]1 = a1[tex]\Psi[/tex]1; A(hat)[tex]\Psi[/tex]2 = a2[tex]\Psi[/tex]2; A(hat)[tex]\Psi[/tex]n = an[tex]\Psi[/tex]n
Calculate: [tex]\left\langle\Psi\left|A(hat)\right|\right\Psi\rangle[/tex]