Discussion Overview
The discussion revolves around the experimental methods to distinguish between two-body and three-body decays in particle physics, specifically focusing on the decays of pions and muons. Participants explore the implications of energy spectra and conservation laws in these decay processes.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
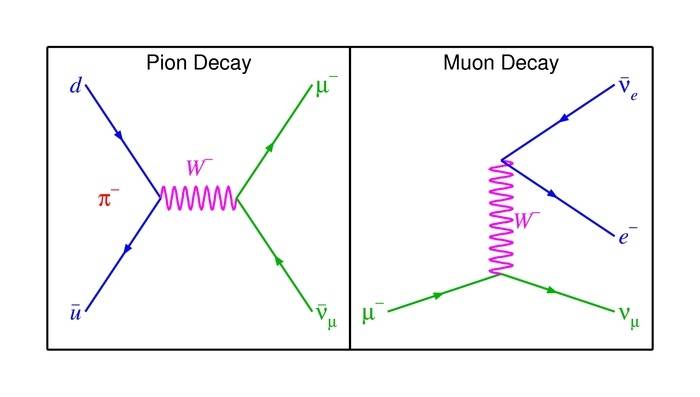
- Some participants inquire about experiments that can differentiate between two-body and three-body decays, particularly in the context of pion and muon decays.
- It is suggested that the energy spectrum of visible decay products can be measured, with two-body decays producing muons at the same energy and three-body decays resulting in a continuous energy spectrum.
- One participant presents a mathematical framework for analyzing the energy of muons in the rest frame of the pion, noting that the energy of the muon is fixed under certain conditions.
- Another participant discusses the implications of momentum conservation in three-body decays, indicating that the momenta of decay products can vary, leading to a continuous spectrum of energies.
- There is a mention of how the difference in degrees of freedom between two-body and three-body decays affects the number of solutions available for momentum and energy conservation equations.
Areas of Agreement / Disagreement
Participants express differing views on the specifics of energy spectra in two-body versus three-body decays, and there is no consensus on the exact nature of the experiments currently being conducted to observe these decays.
Contextual Notes
Some mathematical steps and assumptions in the discussions remain unresolved, and the dependence on specific definitions of decay processes is noted.