- #1
JD_PM
- 1,131
- 158
- TL;DR Summary
- I am computing the decay rate for the pion into a muon and anti-muon neutrino but I do not get the desired expression *, so I would like to discuss the calculation
I am studying the following process: pion decays (mediated by the charged ##W## boson) into a muon and anti-muon neutrino (i.e. ##\pi^- \to \mu + \bar{\nu}_{\mu}##). The Feynman diagram associated to it is
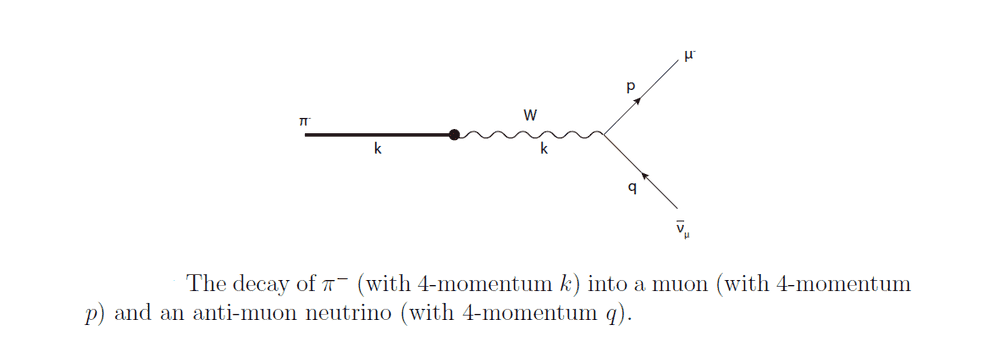 And its Feynman amplitude is (where we of course neglected ##\mathcal{O}(m_{\mu}^2/m_{W}^2)## and higher orders and assumed that the anti-muon neutrino is massless).
And its Feynman amplitude is (where we of course neglected ##\mathcal{O}(m_{\mu}^2/m_{W}^2)## and higher orders and assumed that the anti-muon neutrino is massless).
\begin{equation*}
\mathscr{M} = \frac{g^2}{8 m^2_W}f_{\pi} m_{\mu} \bar{u}_r(\vec p) (1-\gamma_5)v_s (\vec q)
\end{equation*}
I am particularly interested in verifying that the decay rate ##\Gamma## of such process is given by
\begin{equation*}
\Gamma = \frac{g^4 f_{\pi}^2}{256 \pi} \frac{m^2_{\mu}m_{\pi}}{m^4_{W}} \left( 1 - \frac{m^2_{\mu}}{m_{\pi}^2} \right)^2 \tag{*}
\end{equation*}
Let's get started. The differential decay rate is defined by ##d\Gamma := \left| S_{fi}\right|^2 / T##, where the matrix element ##S_{fi}## is given by
\begin{equation*}
S_{fi} = (2 \pi)^4 \delta^{(4)} (k - p - q) \sqrt{\frac{m}{V E_p}} \sqrt{\frac{m}{V E_q}} \sqrt{\frac{1}{2V E_q}} \sum_{r,s} \mathscr{M}
\end{equation*}
Let us first deal with the square of ##\mathscr{M}##; we have
\begin{align*}
\sum_{r,s} \left|\mathscr{M} \right|^2 &= \sum_{r,s} \frac{g^4}{64 m^4_W} f^2_{\pi} m_{\mu}^2 \underbrace{\bar u_r (\vec p) (1-\gamma_5) v_s(\vec q) \bar v_s(\vec q) (1-\gamma_5) u_r (\vec p)}_{\text{we can take the trace}} \\
&= \sum_{r,s} \frac{g^4}{64 m^4_W} f^2_{\pi} m_{\mu}^2 tr \left[\bar u_r (\vec p) (1-\gamma_5) v_s(\vec q) \bar v_s(\vec q) (1-\gamma_5) u_r (\vec p) \right] \\
&= \frac{g^4}{64 m^4_W} f^2_{\pi} m_{\mu}^2 tr \left[(1-\gamma_5) \underbrace{\sum_s v_s(\vec q) \bar v_s(\vec q)}_{(q \!\!/ - m_{\mu})/2m_{\mu}} (1-\gamma_5) \underbrace{\sum_r u_r (\vec p)\bar u_r (\vec p)}_{(q \!\!/ + m_{\mu})/2m_{\mu}} \right] \\
&= \frac{g^4}{256 m^4_W} f^2_{\pi} tr \left[(1-\gamma_5) (q \!\!/ - m_{\mu})(1-\gamma_5)(q \!\!/ + m_{\mu}) \right]
\end{align*}
My issue at this point is how to evaluate such trace.
Using the fact that ##\{ \gamma^{\mu}, \gamma^5 \} = 0## and the following properties
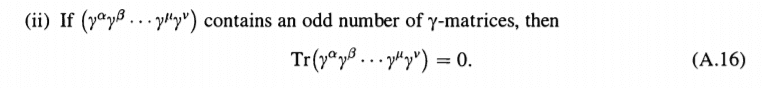
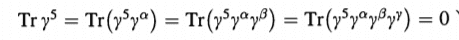
I get
\begin{align*}
&tr\left[(1-\gamma_5)(q \!\!\!/ - m_{\mu})(1-\gamma_5)(p \!\!\!/ + m_{\mu}) \right]\\
&= tr\left[ (q \!\!\!/ (1 + \gamma_5) - m_{\mu}(1 - \gamma_5)) (1-\gamma_5)(p \!\!\!/ + m_{\mu}) \right] \\
&= tr\left[ - m_{\mu}(1 - \gamma_5)^2 (p \!\!\!/ + m_{\mu}) \right] \\
&= -2tr\left[ m_{\mu}(1 - \gamma_5) (p \!\!\!/ + m_{\mu})\right] \\
&= -8 m_{\mu}^2
\end{align*}
However, this does not lead to (*). It seems suspicious to me that momenta terms vanish...
Do you see any mistake so far? If not, the mistake has to be in what follows so I will post the rest of the calculation.
Thank you
PS: I post this specific calculation here because it is directly related to particle physics and I had really good previous experiences in this forum thanks to vanhees71, nrqed & Dr.AbeNikIanEdL
\begin{equation*}
\mathscr{M} = \frac{g^2}{8 m^2_W}f_{\pi} m_{\mu} \bar{u}_r(\vec p) (1-\gamma_5)v_s (\vec q)
\end{equation*}
I am particularly interested in verifying that the decay rate ##\Gamma## of such process is given by
\begin{equation*}
\Gamma = \frac{g^4 f_{\pi}^2}{256 \pi} \frac{m^2_{\mu}m_{\pi}}{m^4_{W}} \left( 1 - \frac{m^2_{\mu}}{m_{\pi}^2} \right)^2 \tag{*}
\end{equation*}
Let's get started. The differential decay rate is defined by ##d\Gamma := \left| S_{fi}\right|^2 / T##, where the matrix element ##S_{fi}## is given by
\begin{equation*}
S_{fi} = (2 \pi)^4 \delta^{(4)} (k - p - q) \sqrt{\frac{m}{V E_p}} \sqrt{\frac{m}{V E_q}} \sqrt{\frac{1}{2V E_q}} \sum_{r,s} \mathscr{M}
\end{equation*}
Let us first deal with the square of ##\mathscr{M}##; we have
\begin{align*}
\sum_{r,s} \left|\mathscr{M} \right|^2 &= \sum_{r,s} \frac{g^4}{64 m^4_W} f^2_{\pi} m_{\mu}^2 \underbrace{\bar u_r (\vec p) (1-\gamma_5) v_s(\vec q) \bar v_s(\vec q) (1-\gamma_5) u_r (\vec p)}_{\text{we can take the trace}} \\
&= \sum_{r,s} \frac{g^4}{64 m^4_W} f^2_{\pi} m_{\mu}^2 tr \left[\bar u_r (\vec p) (1-\gamma_5) v_s(\vec q) \bar v_s(\vec q) (1-\gamma_5) u_r (\vec p) \right] \\
&= \frac{g^4}{64 m^4_W} f^2_{\pi} m_{\mu}^2 tr \left[(1-\gamma_5) \underbrace{\sum_s v_s(\vec q) \bar v_s(\vec q)}_{(q \!\!/ - m_{\mu})/2m_{\mu}} (1-\gamma_5) \underbrace{\sum_r u_r (\vec p)\bar u_r (\vec p)}_{(q \!\!/ + m_{\mu})/2m_{\mu}} \right] \\
&= \frac{g^4}{256 m^4_W} f^2_{\pi} tr \left[(1-\gamma_5) (q \!\!/ - m_{\mu})(1-\gamma_5)(q \!\!/ + m_{\mu}) \right]
\end{align*}
My issue at this point is how to evaluate such trace.
Using the fact that ##\{ \gamma^{\mu}, \gamma^5 \} = 0## and the following properties
I get
\begin{align*}
&tr\left[(1-\gamma_5)(q \!\!\!/ - m_{\mu})(1-\gamma_5)(p \!\!\!/ + m_{\mu}) \right]\\
&= tr\left[ (q \!\!\!/ (1 + \gamma_5) - m_{\mu}(1 - \gamma_5)) (1-\gamma_5)(p \!\!\!/ + m_{\mu}) \right] \\
&= tr\left[ - m_{\mu}(1 - \gamma_5)^2 (p \!\!\!/ + m_{\mu}) \right] \\
&= -2tr\left[ m_{\mu}(1 - \gamma_5) (p \!\!\!/ + m_{\mu})\right] \\
&= -8 m_{\mu}^2
\end{align*}
However, this does not lead to (*). It seems suspicious to me that momenta terms vanish...
Do you see any mistake so far? If not, the mistake has to be in what follows so I will post the rest of the calculation.
Thank you
PS: I post this specific calculation here because it is directly related to particle physics and I had really good previous experiences in this forum thanks to vanhees71, nrqed & Dr.AbeNikIanEdL