Explaining Mesh Currents: Understanding the Relationship between i1 and i2

[rugerts]

Homework Statement

Find the power developed by the dependent voltage source

Relevant Equations

KVL, KCL

Here's my work.

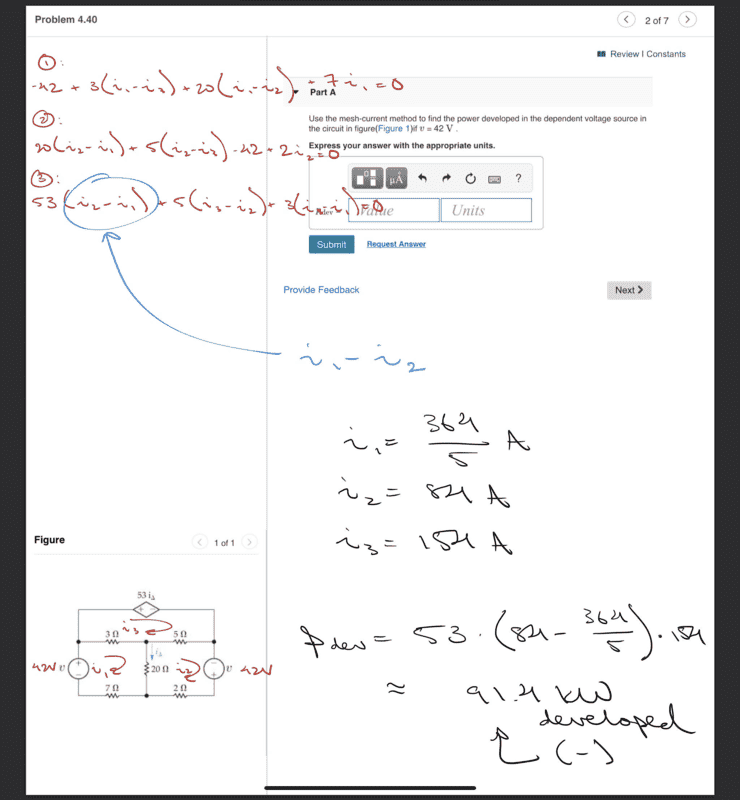
I have the correct answer, but I'd like to know why this only works for (i1-i2) plugged in for i_delta as opposed to what I initially put: i_delta = i2-i1. You can see this in the blue text above versus what I originally had in red.

 

[collinsmark]

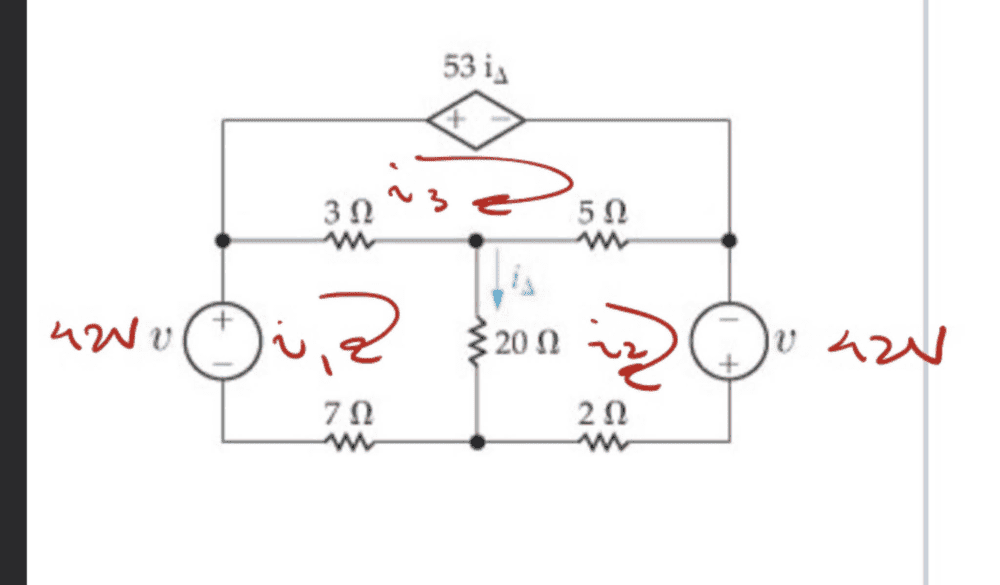
I have the correct answer, but I'd like to know why this only works for (i1-i2) plugged in for i_delta as opposed to what I initially put: i_delta = i2-i1. You can see this in the blue text above versus what I originally had in red.

Each of the following currents (as they are defined), i_1, i_2, and i_\Delta pass through the 20 \ \Omega resistor.

Looking only at a particular current as it passes through the 20 \ \Omega resistor,

Is i_1 in the same direction as i_\Delta, or is it in the opposite direction?

Is i_2 in the same direction as i_\Delta, or is it in the opposite direction?

Given that, how must you define i_\Delta in terms of i_1 and i_2?

 

[rugerts]

Each of the following currents (as they are defined), i_1, i_2, and i_\Delta pass through the 20 \ \Omega resistor.

Looking only at a particular current as it passes through the 20 \ \Omega resistor,

Is i_1 in the same direction as i_\Delta, or is it in the opposite direction?

Is i_2 in the same direction as i_\Delta, or is it in the opposite direction?

Given that, how must you define i_\Delta in terms of i_1 and i_2?

Oh... I see now. Basically i_delta's defined direction gives it all away. Thanks for the reply