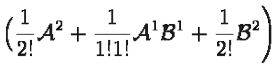The discussion centers around understanding the proof of the exponential operator, specifically the equation e^(A+B) = e^A * e^B. Participants clarify that the proof utilizes power series expansions to demonstrate this relationship, emphasizing the importance of matrix multiplication's distributive property. There is also a focus on the term 1/2!(AB + BA) and how to handle non-commuting matrices in the expansion. Additionally, the conversation shifts to practical steps for calculating the exponential of a matrix, highlighting the conditions under which a matrix can be diagonalized and the implications for finding its exponential. The thread concludes with a discussion on handling matrices that do not have enough independent eigenvectors.