I Explanation of spin degrees of freedom with respect to the x axis

[Somali_Physicist]

Hey Guys/Gals i understand the general premise of this question and can calculate the solution but i am a bit confused.

I am supposed to represent a generic state as a linear combination of the |-,x> , |+,x> basis vectors. However i don't know why, is the question actually asking for the simultaneous eigenstates of energy and the spin observable along the x axis. If that is what it is asking that makes sense as we would be dealing with a state which must be a linear combination of |+,x> , |+,x> then make sure its an eigen state.

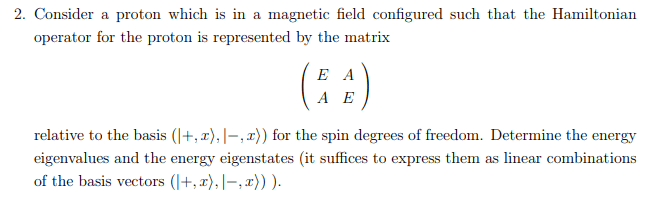
-cheers sarinle

 

[Gaussian97]

Is not asking for the simultaneous eigenstates of spin in the x-direction and the energy (the two operators doesn't commute so it's impossible to find them). You simply have to find the energies and the corresponding eigenstates for the Hamiltonian that they give you.

 

[Somali_Physicist]

Is not asking for the simultaneous eigenstates of spin in the x-direction and the energy (the two operators doesn't commute so it's impossible to find them). You simply have to find the energies and the corresponding eigenstates for the Hamiltonian that they give you.

But in the solution we represent the generic energy eigen vector as a linear combination of |+,x> and |-,x> spin basis states.

|ψ> = a|+,x> + b|-,x>
|ψ>(HMatrix) = c|ψ> : a,b, c are constants

The first statement implies its made up of |+,x> and |-,x> basis states which implies that its an eigen function ... right?

 

[Gaussian97]

But in the solution we represent the generic energy eigen vector as a linear combination of |+,x> and |-,x> spin basis states.

|ψ> = a|+,x> + b|-,x>
|ψ>(HMatrix) = c|ψ> : a,b, c are constants

The first statement implies its made up of |+,x> and |-,x> basis states which implies that its an eigen function ... right?

No, a linear combination of two eigenstates is not necessarily an eigenstate. Since $\left|+,x\right>$ and $\left|-,x\right>$ form a base of the Hilbert space, ANY state can be written as a linear combination of those two (by definition of base).

 

[Somali_Physicist]

No, a linear combination of two eigenstates is not necessarily an eigenstate. Since $\left|+,x\right>$ and $\left|-,x\right>$ form a base of the Hilbert space, ANY state can be written as a linear combination of those two (by definition of base).

I don't wish to be pedantic about this but isn't the hilbert space an infinite dimensional vector space? since the number of basis represent the dimension how can 2 = infinity?

 

[Gaussian97]

No, in the case of spin-1/2 particles the Hilbert space containing the spin states is only 2-dimensional. That's why $H$ is a 2x2 matrix and why you only need two orthonormal states to form a base.

 

[Somali_Physicist]

No, in the case of spin-1/2 particles the Hilbert space containing the spin states is only 2-dimensional. That's why $H$ is a 2x2 matrix and why you only need two orthonormal states to form a base.

So the hilbert space in the case of spin-1/2 particles are 2 dimensional. And i am assuming a new hilbert space can be made for every observable. For instance if we have some X property which has 4 base states we can represent particles with X property construct an hilbert space of 4 dimensions ?

Thanks a lot for the help, i have an exam tomorrow.

 

[Gaussian97]

Well, it's not that you can make a Hilbert space for every new observable, one of the postulates of QP tells you that for any observable there exists an associated hermitian operator that acts on a Hilbert space. But of course, there are several (in fact, infinite) observables that act on the same Hilbert space.
And yes, if you can find a base of only 4 states then your observable is acting on a dimension 4 Hilbert space.

 

[Somali_Physicist]

Well, it's not that you can make a Hilbert space for every new observable, one of the postulates of QP tells you that for any observable there exists an associated hermitian operator that acts on a Hilbert space. But of course, there are several (in fact, infinite) observables that act on the same Hilbert space.
And yes, if you can find a base of only 4 states then your observable is acting on a dimension 4 Hilbert space.

Wow!

so this let's us do some neat trick thanks mate.

 

[andresB]

Just to be sure. The exercise disregard any spatial degree of freedom and focus only on the Spin. For a general case, the total Hilbert space will be the tensor product of spatial degrees of freedom and the Spin.

What the x mean in the exercise is the following:
There is a spin operator for each axis $$
s_{x},s_{y},s_{z}
$$
But, they don't commute with each other. So, you can't find a common basis of eigenvectors. The operator $$
S^{2}=s_{x}^{2}+s_{y}^{2}+s_{z}^{2}$$
do commute with them. Therefore, you can find a basis of vector that are eigenvectors for , let say
$$S^{2},s_{z}$$
let's write this base as $$
\left\{ \left|+,z\right\rangle ,\left|-,z\right\rangle \right\}

$$
where the z means they are eigenvectors of the sz operator. This is normally what is done, and usually the z is missing because it is implcitly understood. But, there is nothing sacred about the z axis, the same can be done with the x axis. There exists a basis
$$ \left\{ \left|+,x\right\rangle ,\left|-,x\right\rangle \right\} $$
of common eigenvectors of
$$ S^{2},s_{x} $$

The two basis are different, but they are related by a linear transformation.