Exploring Radial Forces Generated by Wrapping Strings

[Safety Lab]

Hello all,

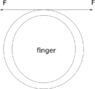
I have been racking my brain with this one all day and I can't seem to figure it out. I have been looking into the forces that would arise from wrapping a string, wire, etc. around your finger. The scenario is illustrated in the attachment. Basically the question is, if we start to pull on both ends of the string with some force, F, eventually the loop will tighten around the finger. I am curious, what kind of radial force would be generated here? If we assume that the finger is not compressible, then a greater and greater force will build the more force we apply at the ends, right? I am basically looking for an equation that would translate a horizontal forces on the ends throughout the loop. I understand that will probably relating the force applied and the angle of loop and what not. If it is a FEM type of question, fine, I just want to figure it out.

THANKS!

 

[jrmichler]

Start by assuming zero friction between the string and the finger. Then the tension in the string is constant along the entire length of the string. Call that tension T.

There is a radial force under the string. That force is expressed as force per unit length - typically pounds per inch or Newtons per meter. Call that force F.

Now make a free body diagram by slicing the finger down the middle so that the string is wrapped 180 degrees. Since this is a free body physics finger, no pain or blood is involved.

Then 2T = F X 2r, where r is the radius of the finger. Solve for F, and F = T / r. It's very similar to the equations for hoop stress in a thin walled pressure vessel.