Darkmisc
- 222
- 31
- Homework Statement
- f(x)=(x+1)^0.5, h(x)=x^2+3, what is the range of f(h(x))?
- Relevant Equations
- f(x)=(x+1)^0.5, h(x)=x^2+3
Hi everyone
I have solutions to this problem, but still don't understand them.
I thought the range of h(x) was [3, \infty). Wouldn't this make the domain of f(h(x)) also [3, infinity)?
If this is correct, shouldn't the range of f(h(x)) be [13^0.5, infinity)?
Below is a graph of f(h(x)) using the assumption that the range of h(x) is [3, infinity)
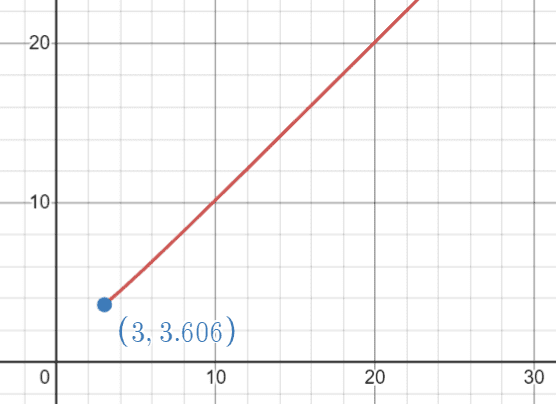
The solutions say
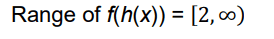
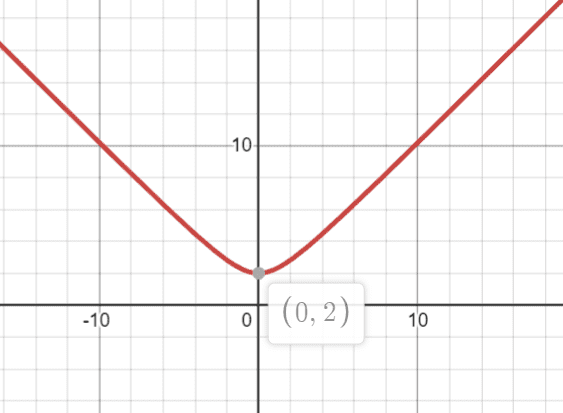
But the domain of f(h(x)) would need to include 0 for this to be true.
 Thanks
Thanks
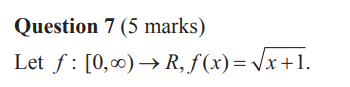
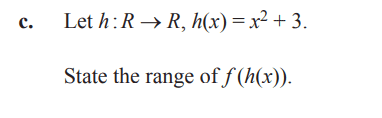
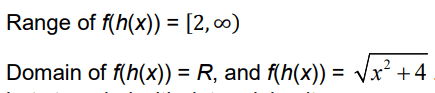
I have solutions to this problem, but still don't understand them.
I thought the range of h(x) was [3, \infty). Wouldn't this make the domain of f(h(x)) also [3, infinity)?
If this is correct, shouldn't the range of f(h(x)) be [13^0.5, infinity)?
Below is a graph of f(h(x)) using the assumption that the range of h(x) is [3, infinity)
The solutions say
But the domain of f(h(x)) would need to include 0 for this to be true.