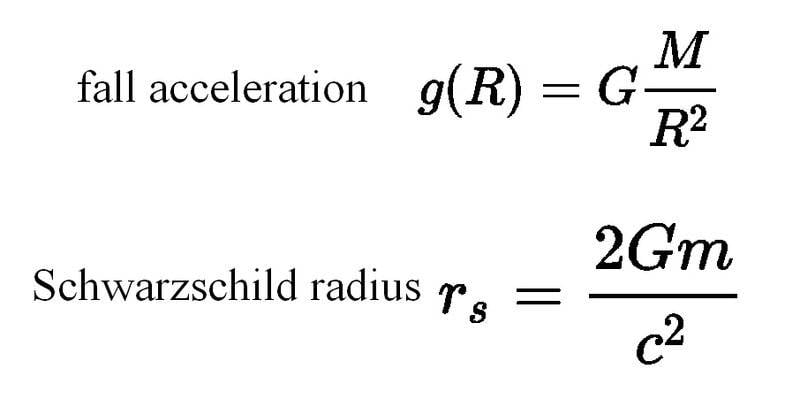SUMMARY
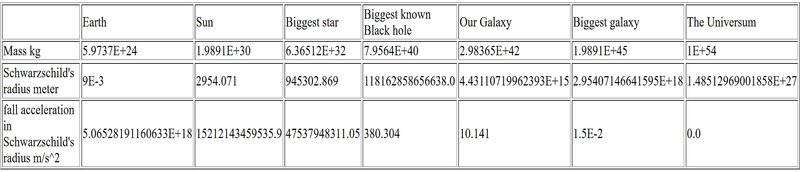
The discussion centers on the characteristics of black holes, specifically the relationship between mass and fall acceleration at the Schwarzschild radius. It is established that the fall acceleration, defined as ##GM / R^2##, does not represent the proper acceleration experienced by an object at that radius. Instead, the proper acceleration is given by ##GM / (R^2 \sqrt{1 - 2GM / (c^2 R)})##. Additionally, the conversation emphasizes that tidal forces, rather than fall acceleration, are more relevant when considering the experience of an observer falling into a black hole, particularly noting that larger black holes exhibit weaker tidal forces.
PREREQUISITES
- Understanding of Schwarzschild radius in general relativity
- Familiarity with gravitational force equations, specifically ##GM / R^2##
- Knowledge of proper acceleration and its calculation
- Concept of tidal forces in the context of black holes
NEXT STEPS
- Research the implications of the Schwarzschild radius on black hole physics
- Study the differences between proper acceleration and coordinate acceleration
- Explore the concept of tidal forces and their effects near black holes
- Investigate the relationship between black hole mass and tidal force strength
USEFUL FOR
Astronomers, physicists, and students of general relativity who are interested in the dynamics of black holes and the effects of mass on gravitational phenomena.