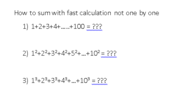MHB Fast Calculation [sum] problem

  • Thread starter Thread starter susanto3311
  • Start date Start date
  • Tags Tags
    Calculation Sum
Click For Summary
SUMMARY

The discussion focuses on solving a problem involving the summation of three mathematical formulas. The formulas provided are: the sum of the first n natural numbers, the sum of the squares of the first n natural numbers, and the sum of the cubes of the first n natural numbers. Specifically, the formulas are: $$\sum_{k=1}^n\left(k\right)=\frac{n(n+1)}{2}$$, $$\sum_{k=1}^n\left(k^2\right)=\frac{n(n+1)(2n+1)}{6}$$, and $$\sum_{k=1}^n\left(k^3\right)=\left(\frac{n(n+1)}{2}\right)^2$$. Participants are encouraged to identify the value of n and compute the sums using these formulas.

PREREQUISITES
  • Understanding of summation notation and basic algebra
  • Familiarity with mathematical series and sequences
  • Knowledge of polynomial expressions and their properties
  • Ability to manipulate and solve equations
NEXT STEPS
  • Research the application of summation formulas in combinatorics
  • Explore advanced topics in mathematical series, such as convergence and divergence
  • Learn about the derivation of summation formulas and their proofs
  • Investigate software tools for symbolic computation, such as Mathematica or Maple
USEFUL FOR

Mathematicians, educators, students studying calculus or algebra, and anyone interested in mathematical problem-solving techniques.

susanto3311
Messages
73
Reaction score
0
hello all...

would you help me out, how to sum 3 questions problem..

please, see my picture attachment..

thanks for your helping...

susanto3311
 

Attachments

  • 3 sum question problem.png
    3 sum question problem.png
    2.3 KB · Views: 84
Mathematics news on Phys.org
There are 3 formulas you can use here:

[box=blue]
Summation Formulas​

$$\sum_{k=1}^n\left(k\right)=\frac{n(n+1)}{2}\tag{1}$$

$$\sum_{k=1}^n\left(k^2\right)=\frac{n(n+1)(2n+1)}{6}\tag{2}$$

$$\sum_{k=1}^n\left(k^3\right)=\left(\frac{n(n+1)}{2}\right)^2\tag{3}$$[/box]

Can you identify $n$ in each case and find the sums?
 

Similar threads

MHB Summing Formula Problem [Again]
  • · Replies 2 ·
Replies
2
Views
1K
MHB Need Sum of Formula [shortcut]
  • · Replies 2 ·
Replies
2
Views
2K
MHB This is known as the Sector Area Formula.
  • · Replies 11 ·
Replies
11
Views
3K
Graduate How to use the Newton-Raphson method while keeping the sum constant?
  • · Replies 2 ·
Replies
2
Views
2K
MHB Find Area Problem in Multiple Choice Question
  • · Replies 5 ·
Replies
5
Views
2K
MHB Looking Answer About Area of Circle.
  • · Replies 4 ·
Replies
4
Views
2K
MHB Find Mean With Multiple Data [Shortcut]
  • · Replies 5 ·
Replies
5
Views
2K
MHB How to Calculate Sold Out Item
  • · Replies 11 ·
Replies
11
Views
4K
MHB How Do You Solve a Geometric Sum with Alternating Signs?
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Find an explicit formula for this n-sum problem
  • · Replies 7 ·
Replies
7
Views
3K