Graduate Solving Maxwell's Equations for Electric Field of AC Wire

[nlis12]

I'm having trouble figuring out how to solve Maxwell's equations for the electric field of an AC wire.

I assume the Voltage waveform in the wire is 120sin(60t). This circuit only has a 14ohm heater in it, according to Ohm's law I=V/R. The current is equation to I(t)=120sin(60t)/14

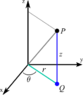
It is common knowledge that a current carrying wire creates a magnetic field in the THETA direction.
This magnetic field is :
B(t)= u_o*I(t)/(2*pi*r) theta direction

Where r is the cylindrical, radial distance from the x axis.

Now plugging in B(t) into ampere's law, I run into trouble when solving for the time varying electric field. Particularly when calculating the curl of B(t). I always get zero.

Am I setting this problem up correctly? Any hints as to where I went wrong?

 

[Gene Naden]

Sure, well the $\nabla \times B$ is not zero because the field is sort of circular. You wrote that it is in the $\theta$ direction. That is correct; if you surround the wire by a circle, the field would be tangent to the circle. Show me how you calculate the curl. Stokes theorem gives a relationship between the curl of B and the the product of $|B|$ times the circumference.

Thanks for your question!

 

[nlis12]

Gene,

Please see this link, this is how I solved the Curl of the Magnetic Field

 

[Gene Naden]

Hi there,
Could you please tell me which way is the Z axis going? And the x and y axes?

It would be easier to use Stokes theorem. You just integrate around a circle.

Regards,
Gene

 

[nlis12]

Here is a diagram of the coordinate system I used.
Theta starts at the positive x-axis and rotates towards the positive y axis.
r = rho , which is the distance away from the z axis.

 

[nlis12]

Hi there,
Could you please tell me which way is the Z axis going? And the x and y axes?

It would be easier to use Stokes theorem. You just integrate around a circle.

Regards,
Gene

I will try stokes theorem!

Thank you for your help!

 

[Gene Naden]

Which way is the current going in your coordinate system, please?

 

[nlis12]

Which way is the current going in your coordinate system, please?

Gene,

In my problem, I stated AC current. The current waveform is modeled by a sinewave, so half the time it is in the positive z axis and half the time it is in the negative z axis.

I guess, I don't understand why you wouldn't just integrate in cylindrical units as opposed to cartesian, because this problem was set up in cylindrical units.

 

[Gene Naden]

Actually, I misled you. $\nabla \times B$ is equal to zero outside the wire. It is only nonzero along the wire where $\rho=0$ (where the current is).

 

[Gene Naden]

So I think your calculation of the curl is correct. And you have the right dependence of the magnetic field on $\rho$. It is inversely proportional. And the magnetic field alternates back and forth as the current alternates. The question in my mind is whether or not this produces an electric field. At low frequencies (like 60 Hz), I would say the electric field is negligible.

You don't say exactly what the statement of the problem is. Did the instructor just say "solve Maxwell's equations" and leave it at that?

Regards,
Gene

 

[Gene Naden]

I just noticed your question about coordinate systems. You are absolutely right; use cylindrical coordinates for this problem.

 

[nlis12]

I just noticed your question about coordinate systems. You are absolutely right; use cylindrical coordinates for this problem.

Thank you for helping me clear this up!
Much appreciated!