Helmholtzerton
- 30
- 4
Hello,
I'm trying to integrate a signal received on an oscilliscope, but I'm afraid using the function cumtrapz is not giving me the correct value. Here is what I'm seeing when testing out sine functions
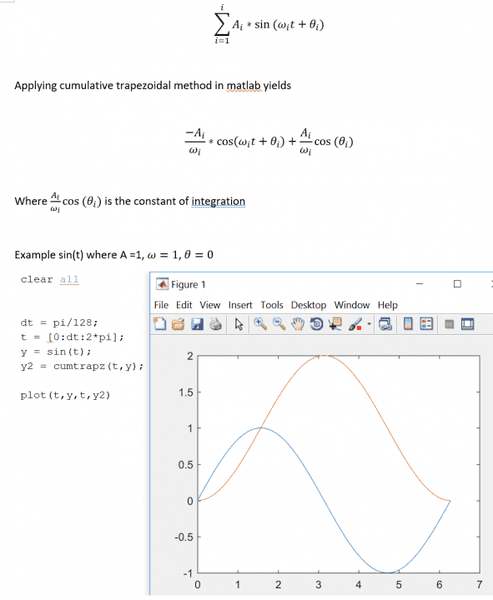
I could apply an FFt to obtain the components and the phases, and then subtract off the constant of integration. However my signals are not clean sineusoids.
Are there any integration techniques I can apply which can subtract off this constant?
I'm trying to integrate a signal received on an oscilliscope, but I'm afraid using the function cumtrapz is not giving me the correct value. Here is what I'm seeing when testing out sine functions
I could apply an FFt to obtain the components and the phases, and then subtract off the constant of integration. However my signals are not clean sineusoids.
Are there any integration techniques I can apply which can subtract off this constant?