Discussion Overview
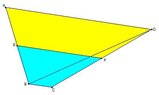
The discussion revolves around finding the area of trapezoid ABCD, where AD is parallel to BC. Participants explore the relationship between the areas of specific regions within the trapezoid and the triangle ABD, using a given area ratio and some geometric properties.
Discussion Character
- Mathematical reasoning
- Debate/contested
- Exploratory
Main Points Raised
- Post 1 introduces the trapezoid and states the area ratio of regions AEFD and EBCF as $(\sqrt 3+1):(3-\sqrt 3)$, along with the area of triangle ABD being $\sqrt 3$.
- Post 2 questions the interpretation of the area ratio, suggesting it seems incorrect based on numerical approximations.
- Post 4 challenges the ratio by asserting that area AEFD should be less than area EBCF, contradicting the ratio provided.
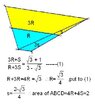
- Post 8 provides a detailed mathematical approach to derive the area of trapezoid ABCD, using variables for the lengths and height, and arrives at an area of 2.
- Post 9 acknowledges a change in the diagram and praises a participant's clever approach to simplify the calculations, suggesting that letting y = 1 reduces the complexity of the problem.
Areas of Agreement / Disagreement
Participants express disagreement regarding the area ratio and its implications, with some questioning the validity of the initial claims. The discussion remains unresolved as different interpretations and methods are presented without consensus.
Contextual Notes
There are limitations regarding the clarity of the diagram and the assumptions made about the areas involved. The discussion also reflects uncertainty about the implications of the area ratio and the relationships between the variables.