Sirmeris1
- 1
- 0
Find cos(z) and sin(z) if z is an angle in quadrant III (in standard position) and the terminal side of angle z is parallel to the line 3x+4y=12.
I just want to make sure I'm thinking about this correctly:
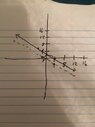
The definition of an angle in standard position is that the vertex is at (0,0) and the the x-axis is one end of the angle. Now, I'm thinking that the line with which the terminal side coincides MUST contain the point (0,0) because the terminal side of an angle must be connected to it's vertex and by definition the vertex of this angle is at (0,0). My problem lies with the fact that if the angle is in quadrant III (which if I remember correctly is the bottom left corner of the Cartesian plane) then the terminal side must also be in quadrant III and the line that contains that terminal side must be parallel to 3x+4y=12 and must contain the point (0,0). But this is impossible, because if a line has the point (0,0) that is parallel to 3x+4y=12 will have the slope -(3/4), from which we get that the line that contains the terminal side is just y=-(3/4)x, but this line doesn't contain any points in quadrant III (because when x is negative y is positive and thus in quadrant II). Therefore, angle z CANNOT have a terminal side in quadrant III parallel to the line 3x+4y=12 because there exists no parallel line to 3x+4y=12 that contains the point (0,0) that also contains points in quadrant III.
So I'm getting that this question is impossible. Is my reasoning flawed here? Am I missing something? Attached is my graph where the solid line is the given line and the line is the theoretical parallel line. Thank you in advance for any clarifications.
View attachment 7022
I just want to make sure I'm thinking about this correctly:
The definition of an angle in standard position is that the vertex is at (0,0) and the the x-axis is one end of the angle. Now, I'm thinking that the line with which the terminal side coincides MUST contain the point (0,0) because the terminal side of an angle must be connected to it's vertex and by definition the vertex of this angle is at (0,0). My problem lies with the fact that if the angle is in quadrant III (which if I remember correctly is the bottom left corner of the Cartesian plane) then the terminal side must also be in quadrant III and the line that contains that terminal side must be parallel to 3x+4y=12 and must contain the point (0,0). But this is impossible, because if a line has the point (0,0) that is parallel to 3x+4y=12 will have the slope -(3/4), from which we get that the line that contains the terminal side is just y=-(3/4)x, but this line doesn't contain any points in quadrant III (because when x is negative y is positive and thus in quadrant II). Therefore, angle z CANNOT have a terminal side in quadrant III parallel to the line 3x+4y=12 because there exists no parallel line to 3x+4y=12 that contains the point (0,0) that also contains points in quadrant III.
So I'm getting that this question is impossible. Is my reasoning flawed here? Am I missing something? Attached is my graph where the solid line is the given line and the line is the theoretical parallel line. Thank you in advance for any clarifications.
View attachment 7022