Find f(x,y) s.t. z=f(x,y) defines a plane in R^3

[gex]

The Question:

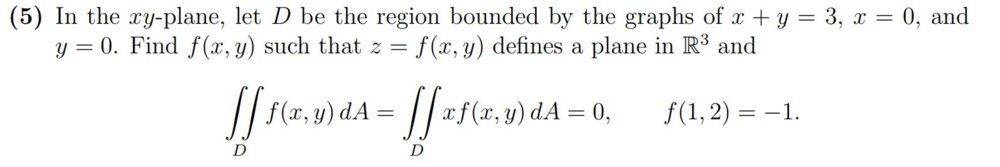
Attempt at a solution:

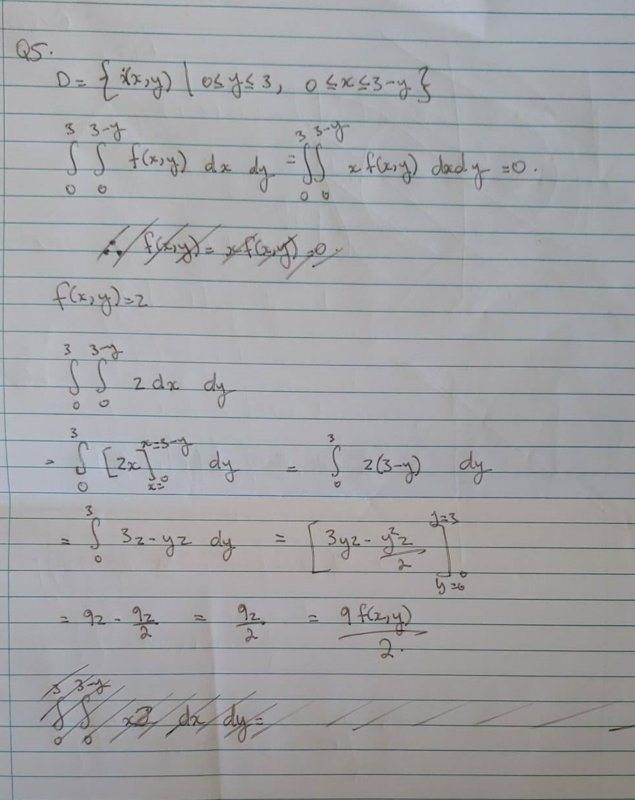
I know for a fact that my attempt is fully wrong, but I am just grasping at straws here and have no clue how to approach this problem. Any help getting me to wrap my head around how to approach this is much appreciated. Thank you in advance.

 

[Ray Vickson]

The Question:
View attachment 240732
Attempt at a solution:
View attachment 240733

I know for a fact that my attempt is fully wrong, but I am just grasping at straws here and have no clue how to approach this problem. Any help getting me to wrap my head around how to approach this is much appreciated. Thank you in advance.

Try setting $f(x,y) = ax + by + c$ for some unknown constants $a,b,c.$ Using your given contitions you can eventually determine $a,b$ and $c$.

 

[gex]

Try setting f(x,y)=ax+by+cf(x,y)=ax+by+cf(x,y) = ax + by + c for some unknown constants a,b,c.a,b,c.a,b,c. Using your given contitions you can eventually determine a,ca,ca,c and ccc.

Thank you so much Ray! I don't know how that didn't cross my mind. I successfully solved the problem now.