Find net external work of a system w/ 2 objects w/ opposite forces

[dcmf]

Homework Statement

Two equal mass blocks are initially at rest and sitting on a frictionless surface. A hand exerts a force of magnitude F on block A, which pushes it to the right by a distance d. Another hand exerts of force of the same magnitude F on block B, which pushes it to the left the same distance d. Consider the blocks A and B as the system. Is the sign of the net external work (Wext) done
by the hands on the system positive, negative, or is it zero?

Relevant Equations

W = Fdcosθ, K = 1/2mv^2, E1+W = E2

A diagram is also provided, which looks like this:

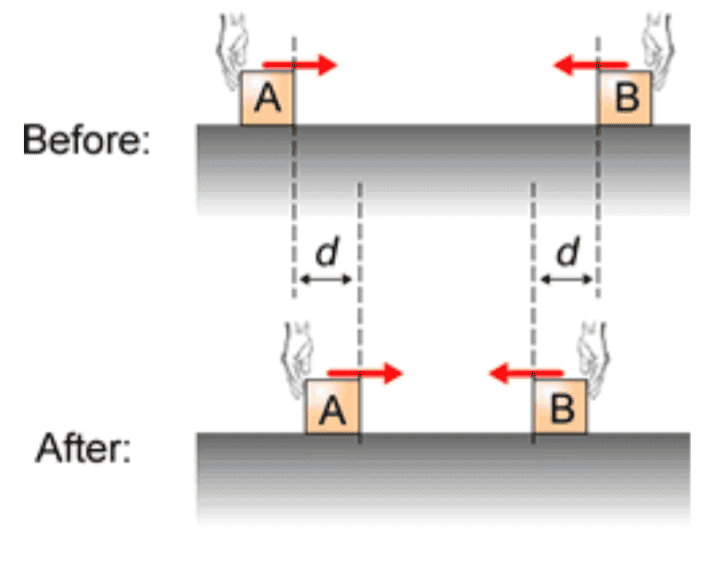
I'm not sure what is correct and after doing some digging online I still haven't been able to come to a consensus. I'm currently stuck between one of two possibilities: positive or zero. I'm pretty sure work on A (Wa) and work on B (Wb) are each positive values (force in same direction as displacement, right??). I also think I getting bogged down by the term "net external work (Wext)" since I'm not 100% sure what this indicates.

Why it might be positive:
If Wa and Wb are positive and Wext is the net external work, I feel like you should be able to just sum up Wa and Wb - making Wext a positive value. Work is a scalar quantity too so there shouldn't be issues with directions being associated with the signs.
Why it might be zero:
At the same time, intuitively it feels like if you consider system A+B, Wa and Wb would cancel each other out somehow because the forces and displacements are equal and opposite to each other. Also would energy equations be valid here (e.g. E1+W = E2) since you're moving the blocks from rest?

 

[BvU]

It's an incomplete problem statement: either there are external forces that stop the blocks, or they are still moving at time 'After'.

Suppose the latter, then external work is positive and it has been converted to kinetic energy.



[edit] expanding/repeating:

Why it might be zero:
At the same time, intuitively it feels like if you consider system A+B, Wa and Wb would cancel each other out somehow because the forces and displacements are equal and opposite to each other.

No, you have established both Wa and Wb to be positive. No canceling.

Also would energy equations be valid here (e.g. E1+W = E2) since you're moving the blocks from rest?

If you mean E1 = kinetic energy of A + kinetic energy of B 'before', E2 = kinetic energy of A kinetic energy of B 'after' then yes,
E1+W = E2 (because there is no friction)
(but please, say what you mean explicitly so there is no confusion).

$\$

 

[kuruman]

It's an incomplete problem statement: either there are external forces that stop the blocks, or they are still moving at time 'After'.

Suppose the latter, then external work is positive and it has been converted to kinetic energy.

$\$

I don't think that the problem statement is incomplete. One doesn't need the "after" picture to determine the sign of the work. While the work is being done on each of the two components of the system and the kinetic energy of each block is increasing, the kinetic energy of the system is increasing. Therefore, the work done on the two-component system is positive. That is sufficient to answer the question.

That said, I should point out that here we have a deformable system, i.e. a system that allows its components to change their relative position under the influence of external forces. When this is the case, the concept of "net work" may become ambiguous because, unless explicitly defined, it may mean two separate quantities.

The first is the sum total of all the works done on the components of the system, $$W_{\text{total}}=\sum_i \mathbf{F}_i\cdot \Delta \mathbf{x}_i=\sum_i\Delta K_i$$and the second is the work done by the net force on the center of mass system, $$W_{\text{net}}=\mathbf{F}_{\text{net}}\cdot\Delta\mathbf{x}_{\text{cm}}.$$The two are not the same when the system is deformable which is why I used different subscripts to distinguish them.

Here, $W_{\text{total}}=2F\Delta x$ where $\Delta x$ is the displacement of each mass whereas $W_{\text{net}}=0.$ One adds kinetic energy to the system but not to the center of mass which is and remains at rest while the forces are applied.

 

[BvU]

I am in favor of the first interpretation -- in order to keep things simple for the OP.
I shudder at the thought of positive work and positive work on the system canceling 'somehow because..'

Work is done on the system, its internal energy increases and the system can do work when returning to its original state.

$\$

 

[kuruman]

am in favor of the first interpretation -- in order to keep things simple for the OP.
I shudder at the thought of positive work and positive work on the system canceling 'somehow because..'

Most certainly, work is not a vector. What "cancels out" are the external forces. I think that the OP has not seen the distinction between rigid and deformable systems.

Note that OP is of two minds: the answer is "positive" but with a nagging intuitive doubt that something is also "zero". I am hopeful that the distinction between the kinetic energy of the system and the kinetic energy of the system's center of mass will sort things out for OP.

 

[hutchphd]

It's an incomplete problem statement: either there are external forces that stop the blocks, or they are still moving at time 'After'.

The problem states "frictionless" and so the inference can be clearly drawn that the blocks remain in motion at t₂. Not incomplete statement IMHO. Each force does positive work on system (A+B). Whether that work ends up as "Kinetic Energy" or internal energy in system (A+B) is not really relevant

 

[dcmf]

Most certainly, work is not a vector. What "cancels out" are the external forces. I think that the OP has not seen the distinction between rigid and deformable systems.

I most definitely have not encountered rigid vs deformable systems yet. Your explanation makes a lot of sense though, thank you very much!

 

[jbriggs444]

The two are not the same when the system is deformable which is why I used different subscripts to distinguish them.

Rotation also provides a case where the sum of the works done by the various forces at various points can differ from the work done by the net force on the center of mass.

 

[kuruman]

Rotation also provides a case where the sum of the works done by the various forces at various points can differ from the work done by the net force on the center of mass.

Yes. The forces acting on this system form a couple except there is no lever arm.