MHB Find Tangent Line w/ Definite Integral - Amy's Question

[MarkFL]

Here is the question:

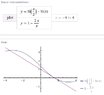
Finding tangent line with definite integral?

Find the equation of the tangent line to the graph of y=A(x) at x= pi/2, where A(x) is defined for all real x by:

A(x)= (sin t/t)dt on the integral x to pi/2

If you could show me all of the steps to finding this, I would be really happy.

Here is a link to the question:

Finding tangent line with definite integral? - Yahoo! Answers

I have posted a link there to this topic so the OP can find my response.

 

[MarkFL]

Hello Amy,

We are given the function:

$$A(x)=\int_x^{\frac{\pi}{2}}\frac{\sin(t)}{t}\,dx$$

and we are asked to find the line tangent to this function at the point:

$$\left(\frac{\pi}{2},A\left(\frac{\pi}{2} \right) \right)=\left(\frac{\pi}{2},0 \right)$$

We know $$A\left(\frac{\pi}{2} \right)=0$$ from the property of definite integrals, demonstrated here by use of the anti-derivative form of the FTOC:

$$\int_a^a f(x)\,dx=F(a)-F(a)=0$$

So, we have the point through which the tangent line must pass, now we need the slope. Using the derivative form of the FTOC, we find:

$$A'(x)=\frac{d}{dx}\int_x^{\frac{\pi}{2}}\frac{\sin(t)}{t}\,dx=-\frac{\sin(x)}{x}$$

Hence:

$$A'\left(\frac{\pi}{2} \right)=-\frac{2}{\pi}$$

We now have a point and the slope, so applying the point-slope formula, we find the equation of the tangent line is:

$$y-0=-\frac{2}{\pi}\left(x-\frac{\pi}{2} \right)$$

$$y=-\frac{2}{\pi}x+1$$

Here is a plot of $A(x)$ and the tangent line:

https://www.physicsforums.com/attachments/811._xfImport

To Amy and any other guests viewing this topic, I invite and encourage you to post other calculus questions here in our http://www.mathhelpboards.com/f10/ forum.

Best Regards,

Mark.