Find the area under the curve

[chwala]

Homework Statement

see attached question and ms

Relevant Equations

integration

Find question here;

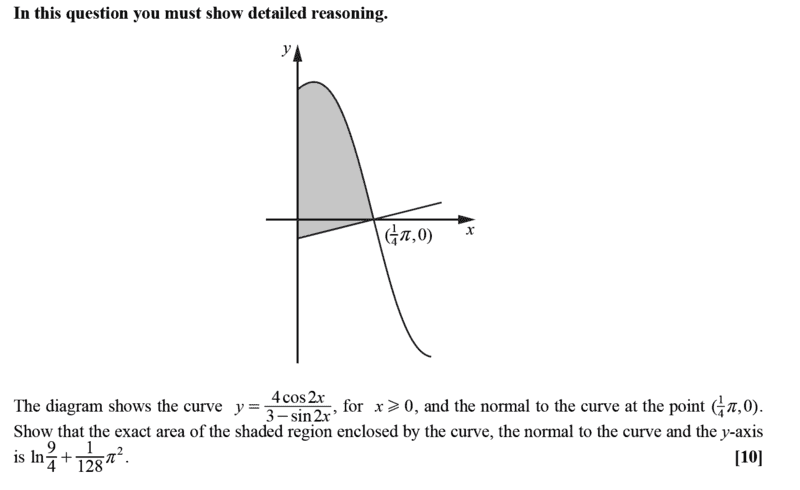
Find solution here;

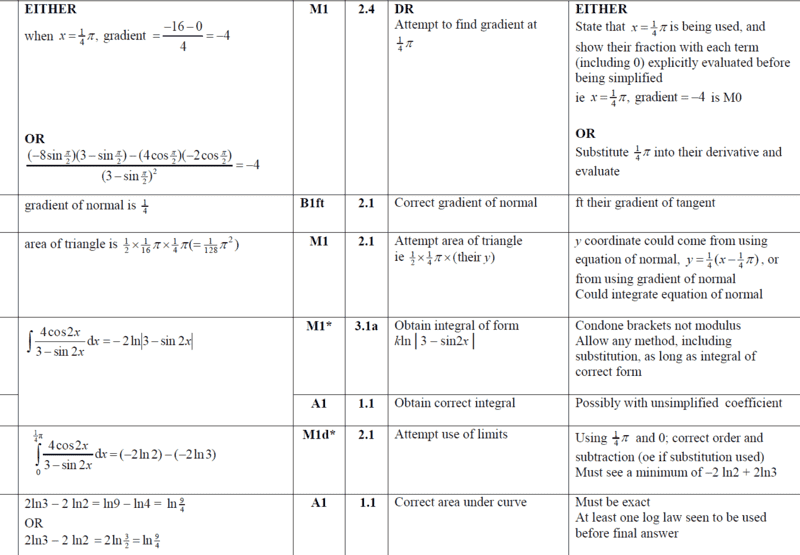
I used the same approach as ms- The key points to me were;

* making use of change of variables...

$$A_{1}=\int_0^\frac{π}{4} {\frac {4\cos 2x}{3-\sin 2x}} dx=-2\int_3^{-2} {\frac {du}{u}}= 2\int_2^3 {\frac {du}{u}}=2\ln 3-2\ln2=\ln 9 - \ln 4=\ln \frac{9}{4}$$

Now to find the other area subtended by the normal, x- axis and y- axis;
We make use of quotient rule. $$y'=\frac{(3-\sin 2x)(-8\sin 2x)-(4\cos 2x)(-2\cos 2x)}{(3-\sin 2x)^2}$$

the x-value =$\frac{π}{4}$ can be substituted here directly and this is what i wanted to share. The gradient of the curve at the point where $x=\frac{π}{4}$ will be
$$y'=\frac{(3-1)(-8)-(0)(0)}{(3-1)^2}=\frac{2⋅-8}{2^2}=-4$$
Now for the given straight line equation, which is a Normal to the curve; We know that,
$y=mx +c$. It follows that,
$0=\frac{1}{4}⋅\frac{π}{4}+c$
$⇒ c=-\frac{π}{16}$
$$A_{2}=\frac {1}{2}⋅\frac{1}{4}⋅ \frac{π}{16}=\frac{π^2}{128}$$
$$A_{Required}= A_{1}+A_{2}=\ln \frac{9}{4}+ \frac{π^2}{128}$$

 

[Master1022]

Apologies, is there a question here? Your answer agrees with the solution - so it looks fine to me...

 

[Delta2]

Apologies, is there a question here? Your answer agrees with the solution - so it looks fine to me...

Sometimes what happens in math solutions, is that you do one mistake, followed by a second mistake and you arrive at a correct result. However I can't find any mistakes in his solution and since it agrees with the official solution, it probably is correct.

 

[chwala]

No question rather just sharing ...as highlighted in blue...maybe I should ask if there is another approach ...particularly on the integrating part of the problem.

 

[neilparker62]

As easy as $\frac{\pi}{4}$

 

[chwala]

We could also integrate by;
Letting $u=\sin 2x$
$$A_{1}=\int_0^\frac{π}{4} {\frac {4\cos 2x}{3-\sin 2x}} dx=2\int_0^1 {\frac {du}{3-u}}=-2\ln(3-1)+2\ln(3-0)=2\ln 3-2\ln2 ...$$