Find the energy which was released when the 'Death Star' was destroyed

[Istiak]

Homework Statement

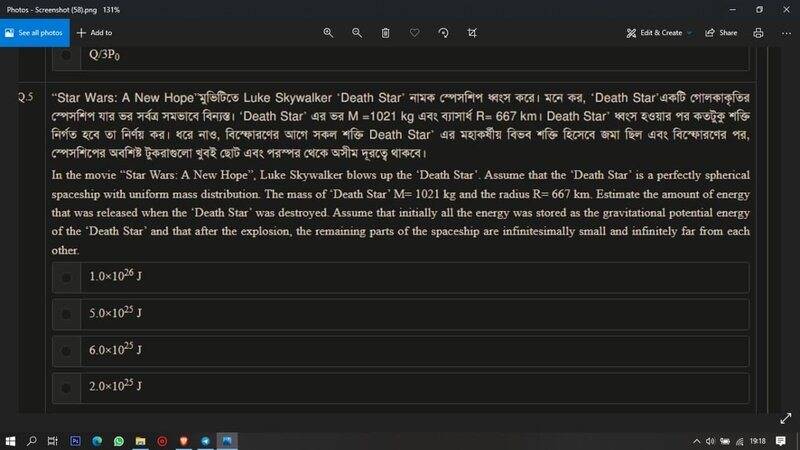
In the movie "Star Wars: A new Hope", Luke Skywalker blows up the 'death star'. Assume that the 'death star' is a perfectly spherical spaceship with uniform mass distribution. The mass of 'Death Star' $M=1021 \mathrm{kg}$ and the radius $R=667\mathrm{km}$ Estimate the amount of the energy that was released when the 'Death Star' was destroyed. Assume that initially all the energy was stored as the gravitational potential energy of the 'Death Star' and that after the explosion, the remaining parts of the spaceship are infinitesimally small and infinitely far from each other

Relevant Equations

E=h\nu

> In the movie "Star Wars: A new Hope", Luke Skywalker blows up the 'death star'. Assume that the 'death star' is a perfectly spherical spaceship with uniform mass distribution. The mass of 'Death Star' $M=1021 \mathrm{kg}$ and the radius $R=667\mathrm{km}$ Estimate the amount of the energy that was released when the 'Death Star' was destroyed. Assume that initially all the energy was stored as the gravitational potential energy of the 'Death Star' and that after the explosion, the remaining parts of the spaceship are infinitesimally small and infinitely far from each other

>>

$E=h\nu$
$E=pc$
$E=h\frac{c}{\lambda}$
$V=mgh$
$E=p\lambda\nu$

And no matter what I do one or two value is always unknown.
$\nu\text{,}\\ \lambda \text{,} \\ p$ frequency, wavelength and momentum respectively.

 

[Bandersnatch]

Neither of these equations is relevant to the problem. The question is about the gravitational energy that binds the entire mass together.
Try looking through your notes for a relevant equation (I don't suspect they'd want you to derive it from scratch).

 

[Istiak]

Neither of these equations is relevant to the problem. The question is about the gravitational energy that binds the entire mass together.
Try looking through your notes for a relevant equation (I don't suspect they'd want you to derive it from scratch).

It's last year Olympiad's question.. I was looking for more equation but couldn't find out...

 

[Bandersnatch]

Are you at all familiar with the concept of binding energy?

 

[Istiak]

Are you at all familiar with the concept of binding energy?

E=mc^2 ? or $\Delta E = \Delta M c^2$
E^2=(mc^2)^2+(pc)^2

If that's what you meant then yes.

 

[Bandersnatch]

No, that's not it (although it is related). We don't need relativity, as this is a classical problem.

You know how it takes some amount of kinetic energy to throw a massive object from the surface of the Earth to infinity? This kinetic energy 'pays for' the equal magnitude of negative potential energy that the body has by the virtue of sitting deep in a gravitational field. That negative potential energy is an example of binding energy associated with - in this case - the gravitational force.
Here, we have a similar situation, but we're not putting a single object away from the central mass - we're putting every bit of mass in the central object away from every other bit. We're unbinding the death star.
Deriving the result requires some calculus, but I suspect the question just wants you to know which equation to use.

I think at this stage it'd be best if you simply went and read about 'gravitational binding energy' e.g. on (English) Wikipedia. You'll find an equation there that you can just plug in the numbers to, together with its derivation. But perhaps more importantly, you should read about what it represents, and try to intuitively understand how it's arrived at, so that you can relate any other similar problem to the concept in the future.

 

[Istiak]

No, that's not it (although it is related). We don't need relativity, as this is a classical problem.

You know how it takes some amount of kinetic energy to throw a massive object from the surface of the Earth to infinity? This kinetic energy 'pays for' the equal magnitude of negative potential energy that the body has by the virtue of sitting deep in a gravitational field. That negative potential energy is an example of binding energy associated with - in this case - the gravitational force.
Here, we have a similar situation, but we're not putting a single object away from the central mass - we're putting every bit of mass in the central object away from every other bit. We're unbinding the death star.
Deriving the result requires some calculus, but I suspect the question just wants you to know which equation to use.

I think at this stage it'd be best if you simply went and read about 'gravitational binding energy' e.g. on (English) Wikipedia. You'll find an equation there that you can just plug in the numbers to, together with its derivation. But perhaps more importantly, you should read about what it represents, and try to intuitively understand how it's arrived at, so that you can relate any other similar problem to the concept in the future.

Thanks; Solved! going to look at GBE.