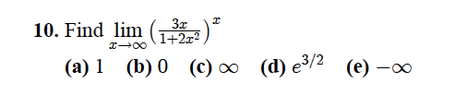Find the limit as x goes to infinity

[Umar]

View attachment 6188Hi, I am having trouble with these kind of questions where we have to use L'Hospital's Rule. I took the ln of the function to get the x out of the exponent, and then followed the Rule by taking the derivative of the top and bottom (using a shortcut we learned: lim x --> infty f(x)g(x) = lim x --> infty f(x) / lim x --> infty g(x).

I got to this point after taking the limits: (infinity) x (- infinity) / (infinity) = 0

where e^(- infinity) = 0 which is the answer.

However, I don't feel confident about the way I simplified those infinities, it doesn't seem right to me. I don't think I have a good understanding of how to deal with those infinites..

Can someone try this question out, and see if you had the same intuition, or is there a different approach I should be taking?

 

[MarkFL]

This limit has the form $0^{\infty}$, and as such is not an indeterminate form, and is simply 0. :D

 

[Umar]

This limit has the form $0^{\infty}$, and as such is not an indeterminate form, and is simply 0. :D

Hmm.. can you explain how you found the limit to be 0 inside of the bracket please?

 

[MarkFL]

Hmm.. can you explain how you found the limit to be 0 inside of the bracket please?

You have inside the brackets:

$$\frac{3x}{1+2x^2}$$

One could simply observe that the degree in the denominator is greater than that of the numerator, and so as $x\to\infty$, this expression goes to 0. This was what I did. Or you can rewrite the expression by dividing both numerator and denominator by $x^2$ to obtain:

$$\frac{\dfrac{3}{x}}{\dfrac{1}{x^2}+2}$$

And we see that as $x\to\infty$, this expressions becomes:

$$\frac{0}{0+2}=0$$

 

[Umar]

You have inside the brackets:

$$\frac{3x}{1+2x^2}$$

One could simply observe that the degree in the denominator is greater than that of the numerator, and so as $x\to\infty$, this expression goes to 0. This was what I did. Or you can rewrite the expression by dividing both numerator and denominator by $x^2$ to obtain:

$$\frac{\dfrac{3}{x}}{\dfrac{1}{x^2}+2}$$

And we see that as $x\to\infty$, this expressions becomes:

$$\frac{0}{0+2}=0$$

Oh wow! I didn't even think of it as simply a rational at first. Can you use that method of dividing all terms by the highest power of x for all rationals?

 

[MarkFL]

Oh wow! I didn't even think of it as simply a rational at first. Can you use that method of dividing all terms by the highest power of x for all rationals?

I don't see why not, for limits as $x\to\pm\infty$. :D