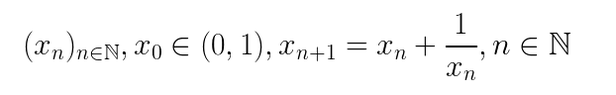Find the Limit of a Sequence: Tips & Techniques
Click For Summary
SUMMARY
The discussion centers on the convergence of a specific mathematical sequence, where participants conclude that the sequence does not converge. The sequence is defined by the recurrence relation $$x_{n+1} = x_n + \frac{1}{x_n}$$. Analysis shows that $$x_n^2 > 2n$$, leading to the conclusion that $$x_n \to \infty$$ as $$n \to \infty$$. Therefore, the sequence diverges, confirming that it does not have a limit.
PREREQUISITES- Understanding of sequences and limits in calculus
- Familiarity with mathematical induction techniques
- Knowledge of convergence and divergence concepts
- Ability to manipulate and analyze recurrence relations
- Study the properties of divergent sequences in calculus
- Learn about mathematical induction and its applications in proving convergence
- Explore the concept of limits in more depth, particularly in relation to sequences
- Investigate other types of recurrence relations and their behaviors
Students and educators in mathematics, particularly those focusing on calculus and analysis, as well as anyone interested in understanding the behavior of sequences and their limits.
Similar threads
- · Replies 1 ·
- · Replies 1 ·
Undergrad
Limits of functions and sequences
- · Replies 36 ·
Undergrad
What is the limit of (a^n)/n for a>1?
- · Replies 7 ·
- · Replies 2 ·
- · Replies 3 ·
- · Replies 7 ·
- · Replies 1 ·
- · Replies 1 ·