paulimerci
- 287
- 47
- Homework Statement
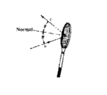
- A tennis ball of mass m rebounds from a racquet with the same speed v as it had
initially as shown. The magnitude of the momentum change of the ball is
(A) 0 (B) 2mv (C) 2mv sin theta (D) 2mv cos theta
- Relevant Equations
- Conservation of momentum
I understand that it is a 2D momentum problem with an elastic collision;
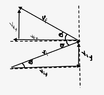
Looking at the vector diagrams below, I notice that the velocity vectors initial and final in the y direction are in the same direction, indicating that momentum does not change, whereas the velocity vectors initial and final in the x direction are opposite each other, indicating that momentum does change.
Therfore,
$$ \Delta p = p_f - p_i$$
$$ = -mvcos\theta -mvcos\theta$$
$$ \Delta p = -2mvcos\theta$$
Have I done it right?
Looking at the vector diagrams below, I notice that the velocity vectors initial and final in the y direction are in the same direction, indicating that momentum does not change, whereas the velocity vectors initial and final in the x direction are opposite each other, indicating that momentum does change.
Therfore,
$$ \Delta p = p_f - p_i$$
$$ = -mvcos\theta -mvcos\theta$$
$$ \Delta p = -2mvcos\theta$$
Have I done it right?