Find the mean and standard deviation of the heights of 13 boys

[chwala]

Homework Statement

see attached

Relevant Equations

statistics

Find the textbook problem here;

Find the textbook solution here:

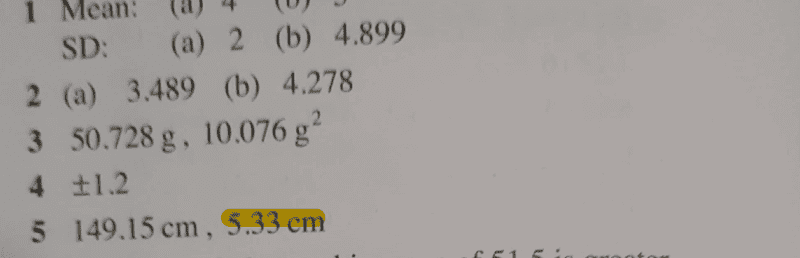Now, to my question, did the textbook guys make an error on the value of $σ?$, see my working;

Mean ($13$ boys)=$\dfrac{153.4+(148.8×12)}{13}=149.15$
We know that,
$29.16$=$\dfrac{\sum x^2}{12}$-$(148.8)^2$
$\sum x^2=266,047.2$
Now, it follows that, $266,047.2+153.4^2=289,578.76$
Variance=$\dfrac{289,578.76}{13}$-$(149.15)^2$
Variance=$29.56673077$
Standard deviation=$\sqrt {29.56673077}=5.4375$

 

[Orodruin]

It seems you forgot to include your work for the standard deviation

 

[Orodruin]

It is generally a bad idea to post before your post is ready and then continue editing it as people will not get notifications of your edits.

Regarding your work, you have used the wrong formula for the variance in a statistical sample where the mean is also estimated from the sample.

 

[chwala]

Ok let me check that...

 

[chwala]

I am unable to see what i have done wrong...i got it! let me post my working...hmmmm

Variance=$\dfrac{\sum (X-x)^2}{N-1}$
$5.4^2$=$\dfrac{\sum (X-x)^2}{11}$
$\sum (X-x)^2$=$320.76$
Therefore,
Variance=$\dfrac{320.76+(153.4-148.8)^2}{12}$
=$\dfrac{341.92}{12}$
=$28.49333333$
Standard deviation=$\sqrt {28.4933333}=5.33$

cheers orodruin...i will make sure to type all my working before posting, my apologies...there may be different approach to this of which i will appreciate...i guess i need more practice here...

 

[Orodruin]

What is N?

 

[chwala]

What is N?

hope you can see it mate

 

[chwala]

Just a question guys, to clear my doubt...the initial number of the boys i.e $12$, is it considered as a sample population or population ?...is sample/population definition dependant on the question? or are we using the fact that data that is less than $30$ items is sample data...
Let me rephrase my question. Supposing the whole class had a total of $12$ boys only. Then is this population or sample data? I can see that the question indicates ' 12 boys in a class' implying population...
cheers

 

[haruspex]

you have used the wrong formula for the variance in a statistical sample

I don’t understand. We are not estimating the mean and variance of a large population of boys from a sample of 12 or 13. In each case, the set of boys is the population. In particular, the mean is exactly known.
I'd say the given answer is wrong.

 

[Orodruin]

I don’t understand. We are not estimating the mean and variance of a large population of boys from a sample of 12 or 13. In each case, the set of boys is the population. In particular, the mean is exactly known.
I'd say the given answer is wrong.

Upon rereading the wording of the problem, I agree. It would have been different if the problem had asked for an estimate of the mean and standard deviation in the height of boys in the age group of the class.

 

[chwala]

So this means the textbook solution is wrong and my initial solution in post $1$ right?

 

[haruspex]

So this means the textbook solution is wrong and my initial solution in post $1$ right?

Yes.

 

[chwala]

Yes.

Bingo!

 

[chwala]

I was just looking at this problem again on my textbook...now i need to amend my textbook solution in Red so as not to fidget around trying to check where i went wrong in my working... i had to check my posts as the problem looked familiar. Hmmmm