Find the Ratio of $\overline{BD}: \overline{CD}$ in $\triangle ABC$

  • Context: MHB 
  • Thread starter Thread starter Albert1
  • Start date Start date
  • Tags Tags
    Ratio
Click For Summary
SUMMARY

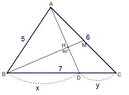
The discussion focuses on finding the ratio of segments $\overline{BD}$ to $\overline{CD}$ in triangle $\triangle ABC$ where $\overline{AB}=5$, $\overline{AC}=6$, and $\overline{BC}=7$. The point $M$ is defined as the midpoint of $\overline{AC}$, and point $D$ lies on $\overline{BC}$ such that $\overline{AD}$ is perpendicular to $\overline{BM}$. The conclusion reached is that the ratio $\overline{BD}:\overline{CD}$ is 5:2.

PREREQUISITES
  • Understanding of triangle properties and segment ratios
  • Knowledge of coordinate geometry and midpoints
  • Familiarity with perpendicular lines and their implications in geometry
  • Basic skills in solving geometric problems involving triangles
NEXT STEPS
  • Study the properties of triangle medians and centroids
  • Learn about the use of coordinate geometry to solve geometric problems
  • Explore the concept of similar triangles and their ratios
  • Investigate the application of the Pythagorean theorem in triangle problems
USEFUL FOR

Students studying geometry, mathematics educators, and anyone interested in solving geometric problems involving triangles and segment ratios.

Albert1
Messages
1,221
Reaction score
0
$\triangle ABC, \overline{AB}=5,\overline{AC}=6,\overline{BC}=7,$$M$ is the midpoint of $\overline{AC}$
$D$ is one point on $\overline{BC}$,if $\overline{AD}\perp \overline{BM}$,
please find the ratio of $\overline{BD}: \overline{CD}$
 

Attachments

  • the ratio of segments BD and CD.jpg
    the ratio of segments BD and CD.jpg
    8 KB · Views: 126
Last edited:
Mathematics news on Phys.org
$$5^2=7^2+6^2-2(7)(6)\cos C\Rightarrow\cos C=\frac57$$

In an orthodiagonal quadrilateral, the sum of the squares of opposite sides are equal, hence

$$x^2+3^2=\overline{MD}^2+5^2\Rightarrow x^2-\overline{MD}^2-16=0\quad[1]$$

$$\overline{MD}^2=9+y^2-2(3)(y)\cos C\Rightarrow\overline{MD}^2=9+y^2-\frac{30}{7}y\quad[2]$$

Substituting $$[2]$$ into $$[1]$$ gives $$x^2- y^2+\frac{30}{7}y-25=0$$

$$7x^2-7y^2+30y-175=0$$

$$7(7-y)^2-7y^2+30y-175=0\Rightarrow y=\frac{42}{17},x=7-y=\frac{77}{17},\frac xy=\frac{11}{6},\overline{BD}:\overline{CD}=11:6$$
 
greg1313 said:
$$5^2=7^2+6^2-2(7)(6)\cos C\Rightarrow\cos C=\frac57$$

In an orthodiagonal quadrilateral, the sum of the squares of opposite sides are equal, hence

$$x^2+3^2=\overline{MD}^2+5^2\Rightarrow x^2-\overline{MD}^2-16=0\quad[1]$$

$$\overline{MD}^2=9+y^2-2(3)(y)\cos C\Rightarrow\overline{MD}^2=9+y^2-\frac{30}{7}y\quad[2]$$

Substituting $$[2]$$ into $$[1]$$ gives $$x^2- y^2+\frac{30}{7}y-25=0$$

$$7x^2-7y^2+30y-175=0$$

$$7(7-y)^2-7y^2+30y-175=0\Rightarrow y=\frac{42}{17},x=7-y=\frac{77}{17},\frac xy=\frac{11}{6},\overline{BD}:\overline{CD}=11:6$$
very good , your answer is right!
 

Similar threads

MHB Proving the Similarity of Two Acute Triangles with Perpendicular Lines
  • · Replies 2 ·
Replies
2
Views
2K
MHB What is the value of Angle BAD in a trapezoid with specific conditions?
  • · Replies 2 ·
Replies
2
Views
2K
MHB Finding $\angle ADC$ in $\triangle ABC$
  • · Replies 3 ·
Replies
3
Views
2K
MHB Can AC^2 be Proven to Equal AB(AB+BC) in Triangle ABC with Angles B=80 and C=40?
  • · Replies 3 ·
Replies
3
Views
2K
MHB Calculating Ratio of $\overline{BP}$ to $\overline {PN}$ in Hexagon $ABCDEF$
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Help finding a triangle inside a triangle
  • · Replies 5 ·
Replies
5
Views
2K
MHB Finding Angle C in Triangle ABC
  • · Replies 3 ·
Replies
3
Views
2K
MHB Finding $\overline {AD} \times \overline {CD}$ in $\triangle APB$
  • · Replies 3 ·
Replies
3
Views
2K
MHB Minimum Perimeter of a Trapezoid: Find R & P
  • · Replies 5 ·
Replies
5
Views
2K
MHB Finding $\angle ACB$ in $\triangle ABC$
  • · Replies 4 ·
Replies
4
Views
2K