evinda
Gold Member
MHB
- 3,741
- 0
Hi! (Nerd)
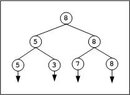
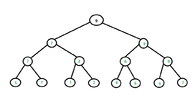
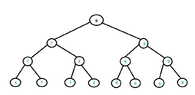
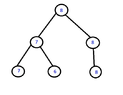
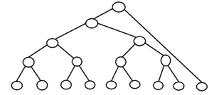
Show that,given a set of numbers $S$,we can count the second smallest element of $S$ with $n+ \lceil \lg n \rceil-2$ comparisons at the worst case.
Hint: Find the smallest element,considering a tournament tree for its finding.
I don't really know how to use the hint.. (Sweating) Could you help me? (Blush)
Show that,given a set of numbers $S$,we can count the second smallest element of $S$ with $n+ \lceil \lg n \rceil-2$ comparisons at the worst case.
Hint: Find the smallest element,considering a tournament tree for its finding.
I don't really know how to use the hint.. (Sweating) Could you help me? (Blush)