Find the second smallest element

[I like Serena]

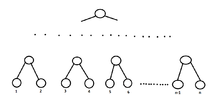
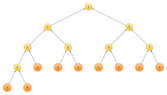
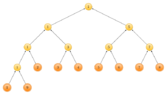
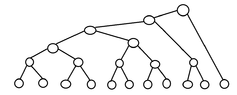
We need $\lceil \lg n \rceil-1=2$ comparisons, to find number two, right? (Thinking)

Yup!

So...? (Sweating)

 

[evinda]

Yup!

So...? (Sweating)

So,we need $n-1+ \lfloor \lg n \rfloor-1=n+ \lfloor \lg n \rfloor -2$ comparisons,right? (Happy)

So, to show that from a given set of numbers with $n$ elements, we can count the second smallest element with $n+ \lceil lgn \rceil−2$ comparisons, can I show it for $n=8$ and then conclude from that the needed number of comparisons for a general $n$ ? Or do I have to do also something else? (Thinking)

 

[I like Serena]

So,we need $n-1+ \lfloor \lg n \rfloor-1=n+ \lfloor \lg n \rfloor -2$ comparisons,right? (Happy)

So, to show that from a given set of numbers with $n$ elements, we can count the second smallest element with $n+ \lceil lgn \rceil−2$ comparisons, can I show it for $n=8$ and then conclude from that the needed number of comparisons for a general $n$ ? Or do I have to do also something else? (Thinking)

Ah well, I guess you still need to prove it.
How would you prove it? (Wondering)

 

[evinda]

Ah well, I guess you still need to prove it.
How would you prove it? (Wondering)

I don't know, maybe using induction? (Thinking)

 

[I like Serena]

I don't know, maybe using induction? (Thinking)

Sounds good... (Smirk)

 

[evinda]

Sounds good... (Smirk)

For $n=2$,we need one comparison to find the second smallest element.

$$n+ \lceil \lg n \rceil -2=2+\lceil \lg 2 \rceil-2=1 \checkmark $$

Then, we suppose that, when we have $n$ elements, we need $n+ \lceil \lg n \rceil -2$ comparisons to find the second smallest element.

But..what happens if we have $n+1$ elements? Do we have to compare the $(n+1)^{th}$ element with the second smallest, that we found above and pick the smallest of them? (Thinking)
Or can't we verify the formula like that? (Sweating)

 

[I like Serena]

For $n=2$,we need one comparison to find the second smallest element.

$$n+ \lceil \lg n \rceil -2=2+\lceil \lg 2 \rceil-2=1 \checkmark $$

Good! (Smile)

Then, we suppose that, when we have $n$ elements, we need $n+ \lceil \lg n \rceil -2$ comparisons to find the second smallest element.

But..what happens if we have $n+1$ elements? Do we have to compare the $(n+1)^{th}$ element with the second smallest, that we found above and pick the smallest of them? (Thinking)
Or can't we verify the formula like that? (Sweating)

We will have to distinguish two cases for $n+1$.

Let's select a complete binary tree for $n$.
When we add leaf $n+1$, there are 2 possibilities.
Either it fits in the last level, or we need to add a new level to accommodate $n+1$.
What happens in those cases to the number of comparisons for first place, respectively second place? (Wondering)

 

[evinda]

We will have to distinguish two cases for $n+1$.

Let's select a complete binary tree for $n$.
When we add leaf $n+1$, there are 2 possibilities.
Either it fits in the last level, or we need to add a new level to accommodate $n+1$.
What happens in those cases to the number of comparisons for first place, respectively second place? (Wondering)

So, don't we consider the tournament tree, proving that we need $n+ \lceil \lg n\rceil-2$ comparisons, by induction? (Sweating) (Thinking)

 

[I like Serena]

So, don't we consider the tournament tree, proving that we need $n+ \lceil \lg n\rceil-2$ comparisons, by induction? (Sweating) (Thinking)

Yes we do.
What's stopping you? (Worried)

 

[evinda]

Yes we do.
What's stopping you? (Worried)

So, when we have $n$ elements, the tournament tree is of this form:

View attachment 3207

and we suppose that we need $n+ \lceil \lg n \rceil-2$ comparisons, in order to find the second smallest element.

But.. what do we do, when we add the $(n+1)^{th}$ element, to show that in this case we need $n+1+ \lceil \lg{ (n+1) } \rceil-2=n+ \lceil \lg{ (n+1) } \rceil-1$ comparisons, for the finding of the second smallest element? (Thinking) (Sweating)

 

[I like Serena]

So, when we have $n$ elements, the tournament tree is of this form:

and we suppose that we need $n+ \lceil \lg n \rceil-2$ comparisons, in order to find the second smallest element.

But.. what do we do, when we add the $(n+1)^{th}$ element, to show that in this case we need $n+1+ \lceil \lg{ (n+1) } \rceil-2=n+ \lceil \lg{ (n+1) } \rceil-1$ comparisons, for the finding of the second smallest element? (Thinking) (Sweating)

In the first case we have a tournament tree that is not a full binary tree, but only a complete binary tree.

When we add leaf $(n+1)$, we need $1$ more comparison to find first place.

Since the tree was not a full binary tree yet, the number of levels stays the same.
Therefore the (worst case) number of comparisons for second place also stays the same.

Therefore the formula $(n+1) + \lceil \lg{ (n+1) } \rceil - 2$ is satisfied. (Wait)

 

[evinda]

In the first case we have a tournament tree that is not a full binary tree, but only a complete binary tree.

Could you explain it further to me, why the tournament tree above is not a full binary tree, but only a complete binary tree? (Sweating)

 

[I like Serena]

Could you explain it further to me, why the tournament tree above is not a full binary tree, but only a complete binary tree? (Sweating)

This is the first of the 2 cases I'm distinguishing.
Either $n$ is of the form $2^k$ or it is not.

If $n$ is not a power of 2, we can set up a tournament tree that is a complete binary tree, but is not a full binary tree. (Wasntme)

 

[evinda]

This is the first of the 2 cases I'm distinguishing.
Either $n$ is of the form $2^k$ or it is not.

If $n$ is not a power of 2, we can set up a tournament tree that is a complete binary tree, but is not a full binary tree. (Wasntme)

A binary tree is full if each node is either a leaf or possesses exactly two child nodes.

A binary tree with $n$ levels is complete if all levels except possibly the last are completely full, and the last level has all its nodes to the left side.

Right? (Thinking)

So, if $n$ is not a power of $2$, don't we have then a full binary tree, and not a complete one? (Thinking) Or have I understood it wrong? (Sweating)

 

[I like Serena]

A binary tree is full if each node is either a leaf or possesses exactly two child nodes.

A binary tree with $n$ levels is complete if all levels except possibly the last are completely full, and the last level has all its nodes to the left side.

Right? (Thinking)

Right! (Yes)

So, if $n$ is not a power of $2$, don't we have then a full binary tree, and not a complete one? (Thinking) Or have I understood it wrong? (Sweating)

It's the other way around.

 

[evinda]

It's the other way around.

For $n=9$, we have, for example, this tournament tree, right?

View attachment 3208

Why is it a complete binary tree, but not a full one? (Thinking)

 

[I like Serena]

For $n=9$, we have, for example, this tournament tree, right?

Why is it a complete binary tree, but not a full one? (Thinking)

It is neither, because node $\enclose{circle}9$ is really at level 2 instead of on the last level.

The complete binary tree is:
View attachment 3209
And it's not a full binary tree since the last level is not fully occupied. (Shake)

 

[evinda]

It is neither, because node $\enclose{circle}9$ is really at level 2 instead of on the last level.

The complete binary tree is:
https://www.physicsforums.com/attachments/3209
And it's not a full binary tree since the last level is not fully occupied. (Shake)

So, do we have to compare the $(n+1)^{th}$ element with the smallest, that we found, when we had $n$ elements?
If so, then if it is greater, then we need one comparison, right?

And.. if it is smaller than the smallest that we found, do we need again only one comparison, since the new smaller element gets the position of the previous one? (Thinking)

 

[I like Serena]

So, do we have to compare the $(n+1)^{th}$ element with the smallest, that we found, when we had $n$ elements?
If so, then if it is greater, then we need one comparison, right?

And.. if it is smaller than the smallest that we found, do we need again only one comparison, since the new smaller element gets the position of the previous one? (Thinking)

I may have gone overboard when creating the tree. (Blush)

It's not supposed to be sorted.
It was just easiest to do it that way.

We just need to slide element $(n+1)$ in somewhere so that we still have a complete binary tree.
That is always possible and will take exactly $1$ more comparison to figure out number one.

 

[evinda]

It's not supposed to be sorted.
It was just easiest to do it that way.

We just need to slide element $(n+1)$ in somewhere so that we still have a complete binary tree.
That is always possible and will take exactly $1$ more comparison to figure out number one.

Could you give me an example? (Thinking)

 

[I like Serena]

Could you give me an example? (Thinking)

What example can you think of? (Wasntme)

 

[evinda]

What example can you think of? (Wasntme)

Having the tournament tree for $n$ elements,where can I place the $(n+1)^{th}$ element? (Thinking)

 

[I like Serena]

Having the tournament tree for $n$ elements,where can I place the $(n+1)^{th}$ element? (Thinking)

Two cases.
If $n$ is of the form $2^k$, you'll need another level and do what I showed in my tree.
Or if $n$ is not of the form $2^k$, you can add it to the right of the last leaf. (Tauri)

 

[evinda]

Two cases.
If $n$ is of the form $2^k$, you'll need another level and do what I showed in my tree.
Or if $n$ is not of the form $2^k$, you can add it to the right of the last leaf. (Tauri)

So, if we have $m$ elements and we want to create a tournament tree, doesn't all the $m$ elements have to be firstly at the same level, that is the last one?

Because, if we have $n+1$ elements, we compare the $(n+1)^{th}$ element with the smallest that we found before when we had $n$ elements,and pick one of them, and then we only have $n$ elements at the same level..

 

[I like Serena]

So, if we have $m$ elements and we want to create a tournament tree, doesn't all the $m$ elements have to be firstly at the same level, that is the last one?

No!
That only works if we happen to have a power of 2.
What if we don't? (Wait)

Because, if we have $n+1$ elements, we compare the $(n+1)^{th}$ element with the smallest that we found before when we had $n$ elements,and pick one of them, and then we only have $n$ elements at the same level..

Huh?

We don't have to compare $(n+1)$ with the smallest.
We only have to add it to the tree.
The exact comparisons may change, but the total number of comparisons will be 1 more than it was before. (Wasntme)

 

[evinda]

No!
That only works if we happen to have a power of 2.
What if we don't? (Wait)

So, what do we have to do, when we have $n=11$ ? $11$ is not a power of $2$, neither $n-1=10$ is.. (Worried)

Huh?

We don't have to compare $(n+1)$ with the smallest.
We only have to add it to the three.
The exact comparisons may change, but the total number of comparisons will be 1 more than it was before. (Wasntme)

So, at the binary tree, that you created, don't we have to compare only $9$ with $1$ ? (Sweating)

View attachment 3240

 

[I like Serena]

So, what do we have to do, when we have $n=11$ ? $11$ is not a power of $2$, neither $n-1=10$ is.. (Worried)

Can you create a tree for that? (Wondering)

So, at the binary tree, that you created, don't we have to compare only $9$ with $1$ ? (Sweating)

Not really. We can shuffle the leaves around any way we like. (Dance)

 

[evinda]

Can you create a tree for that? (Wondering)

I thought that it would be like that:

View attachment 3244

So, is it wrong? (Thinking) Do we have to put the first $2^3=8$ elements at the same level and the remaining $11-8=3$ elements at the next level?

Not really. We can shuffle the leaves around any way we like. (Dance)

How could we do it otherwise? (Worried)

 

[evinda]

I have an idea! (Nerd)

Can we prove the sentence, using strong induction? (Wait)

We will show that with at most $ n + \lceil \lg{n}\rceil - 2$ comparisons we can find the smallest and the second smallest element.

The sentence is true for $n=2$ $\checkmark$ .

We suppose that it stands $\forall 2<k<n$.

Now, we distinguish cases:

• If $n=2m$, we split the elements into $m$ pairs , needing $m$ comparisons.
  
  From each comparison, we pick the smallest number.
  
  From the inductive step, we know that we need at most $m + \lceil \lg{m}\rceil - 2$ comparisons, in order to find the smallest and the second smallest element from the remaining numbers, let $d,e$, with $d<e$.
  
  Also, suppose that at the first $m$ comparisons, $d$ was compared with $d'$.
  
  Then, the smallest element of the initial set of numbers is $d$, and the second smallest element is either $e$ or $d'$.
  
  With one more comparison, we can find which of these two elements is smaller.
  
  In total, we needed:
  
  $$m + (m + \lceil \lg{m}\rceil - 2) + 1 = 2m + \lceil \lg{m} + 1\rceil -2 = n + \lceil \lg{n}\rceil - 2$$
  comparisons.
  $$$$
• Similarly, if $n=2m+1$, we split the elements into $m$ pairs and we leave an element alone .
  
  After $m$ comparisons, we have the smallest $m$ elements and the one that we have left alone , and then with $(m+1) + \lceil \lg{(m+1)}\rceil - 2$ comparisons , we find the smallest and the second smallest from the $m+1$ elements.
  
  Finally, with at most one comparison we find the smallest and the second smallest element of the initial set of numbers. In total, we needed
  $$$$
  $$m + (m+1 + \lceil \lg{(m+1)}\rceil - 2) + 1 = 2m+1 + \lceil \lg{(m+1)} + 1\rceil -2 \\ = n+ \lceil \lg { \left ( \frac{2m+2}{2}\right )+1 \rceil}-2=n+ \lceil \lg { (2m+2} ) \rceil-2= n+ \lceil \lg { (n+1} ) \rceil-2$$
  comparisons.

Is it right so far? Also, how can I show that $n+ \lceil \lg { (n+1} ) \rceil-2$ is equal to $n+ \lceil \lg { n} \rceil-2$ ? (Thinking)