propvgvnda
- 22
- 0
- Homework Statement
- Below
- Relevant Equations
- How to analyze Electric Circuits
Find the supply voltage of a ladder circuit shown, so that I=7A. Assume R=11Ω. (The unit must be placed)
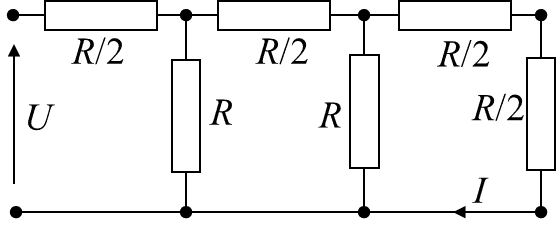
Hello, everyone. Please, help me with this. Could someone explain to me how to solve such tasks. I literally spent the whole day watching Khan Academy and trying to figure out how to solve these circuits, but still, I can't do a thing. I would also be very glad if someone shared a link to some article about this, I have to solve an awful lot of such tasks and I really need to learn how to deal with them. ASAP
Hello, everyone. Please, help me with this. Could someone explain to me how to solve such tasks. I literally spent the whole day watching Khan Academy and trying to figure out how to solve these circuits, but still, I can't do a thing. I would also be very glad if someone shared a link to some article about this, I have to solve an awful lot of such tasks and I really need to learn how to deal with them. ASAP