- #1
zenterix
- 480
- 70
- Homework Statement
- I was trying to understand what an open-circuit voltage is so I looked it up on Wikipedia.
- Relevant Equations
- There is an example there that is the following.
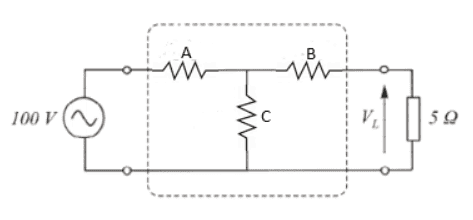
Consider the circuit (Wikipedia, Open Circuit Voltage)
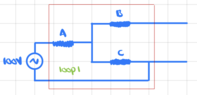
I am having a bit of difficulty understanding the steps and concepts here.
I redrew the circuit as follows
The red square is the same piece of the circuit with the dotted lines around it in the original diagram (not sure what this is for though).
It is not clear to me why there is no current through resistor B. This is my main question.
Assuming that this is true, then the current will be the same everywhere in loop 1 and resistors A and C are in series so
$$R_{eq} = R_A+R_C$$
and we obtain the current as
$$i=\frac{V}{R_{eq}}=\frac{V}{R_A+R_C}$$
We can find the potential drop through C from
$$V-R_Ai-R_Ci=0$$
$$R_Ci=V-R_Ai=V-\frac{R_AV}{R_A+R_C}=\frac{VR_C}{R_A+R_C}$$
which agrees with Wikipedia.
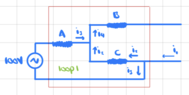
If we want to find the open-circuit voltage across the 5##\Omega## resistor, first disconnect it from the circuit:
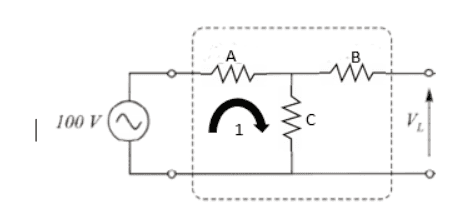
Find the equivalent resistance in loop 1 to find the current in loop 1. Use Ohm's law with that current to find the potential drop across the resistance C. Note that since no current is flowing through resistor B, there is no potential drop across it, so it does not affect the open-circuit voltage.
The open-circuit voltage is the potential drop across the resistance C, which is: ##\frac{C}{C+A}100V_{~}##
I am having a bit of difficulty understanding the steps and concepts here.
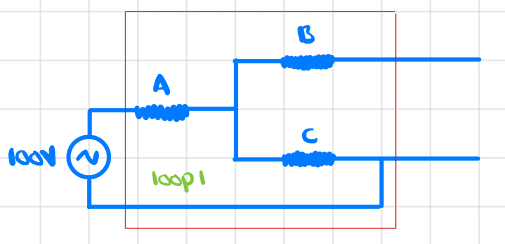
I redrew the circuit as follows
The red square is the same piece of the circuit with the dotted lines around it in the original diagram (not sure what this is for though).
It is not clear to me why there is no current through resistor B. This is my main question.
Assuming that this is true, then the current will be the same everywhere in loop 1 and resistors A and C are in series so
$$R_{eq} = R_A+R_C$$
and we obtain the current as
$$i=\frac{V}{R_{eq}}=\frac{V}{R_A+R_C}$$
We can find the potential drop through C from
$$V-R_Ai-R_Ci=0$$
$$R_Ci=V-R_Ai=V-\frac{R_AV}{R_A+R_C}=\frac{VR_C}{R_A+R_C}$$
which agrees with Wikipedia.