- #1
chwala
Gold Member
- 2,828
- 420
- Homework Statement
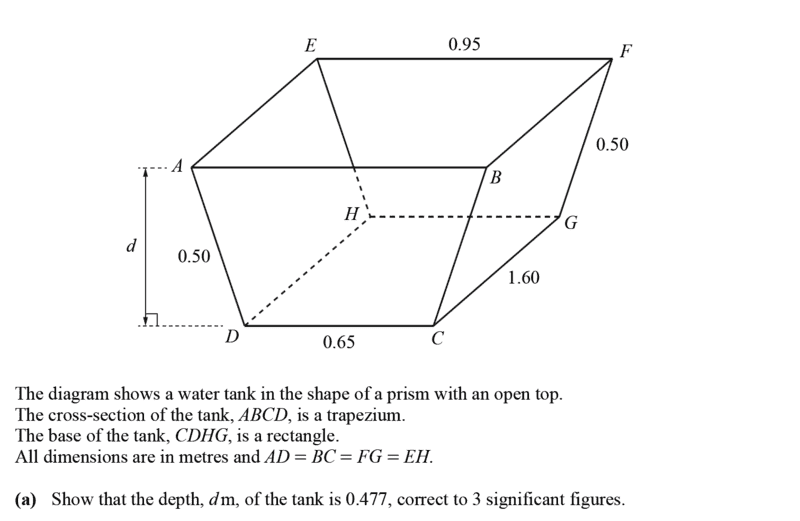
- See attached ( past paper question)
- Relevant Equations
- Knowledge of prisms
My query in only on the highlighted part...c.ii.
Find the question below;
Find the markscheme here
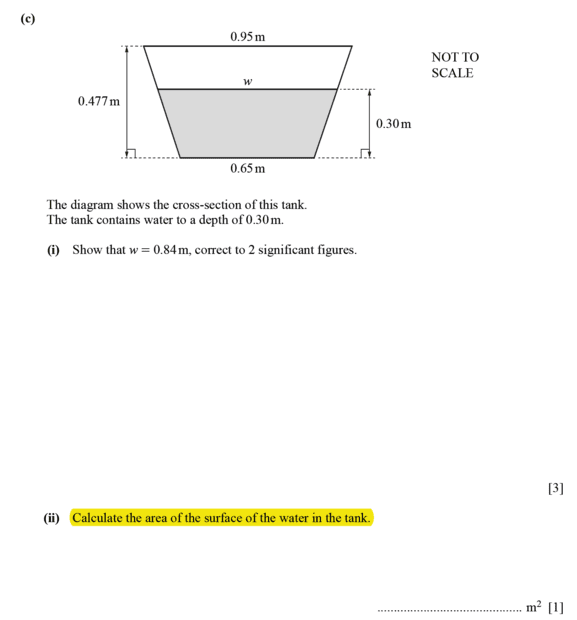
part c(ii) does not seem correct as i have;
##A_1=0.5 ×(0.65+0.84)0.3 ×2=0.447m^2##
##A_2 = 0.65 ×1.6=1.04m^2##
##A_3 = (0.3146 × 1.6)2=1.00672m^2##
Total surface area = ##A_1+A_2+A_3=0.447+1.04+1.00672=2.494m^2##...
For part c.(i), i was able to use similarity (i used a right angle triangle from the cross-section) to show that,
i.e ##\dfrac {0.477}{0.15}##=##\dfrac {0.3}{x}##
##x=0.094## therefore, ##w = 0.65+2(0.094)=0.8386≈0.84## to3 2 significant figures.
Find the question below;
Find the markscheme here
##A_1=0.5 ×(0.65+0.84)0.3 ×2=0.447m^2##
##A_2 = 0.65 ×1.6=1.04m^2##
##A_3 = (0.3146 × 1.6)2=1.00672m^2##
Total surface area = ##A_1+A_2+A_3=0.447+1.04+1.00672=2.494m^2##...
For part c.(i), i was able to use similarity (i used a right angle triangle from the cross-section) to show that,
i.e ##\dfrac {0.477}{0.15}##=##\dfrac {0.3}{x}##
##x=0.094## therefore, ##w = 0.65+2(0.094)=0.8386≈0.84## to
Last edited:
...to two significant figures...yeah, i know that. cheers bvu...