SUMMARY
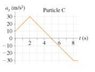
The discussion focuses on calculating the velocity of a particle at 7 seconds using an acceleration versus time graph. The user attempts to integrate the acceleration values over specified intervals, specifically from 0 to 5 seconds, resulting in a total area of -50. The conversation emphasizes the importance of understanding the concept of area under the curve, particularly distinguishing between positive and negative areas, to accurately determine the velocity. The user expresses confusion about how to handle areas above and below the axis, indicating a need for clarity on integration techniques in this context.
PREREQUISITES
- Understanding of integration techniques in calculus
- Familiarity with acceleration versus time graphs
- Knowledge of how to calculate area under a curve
- Basic concepts of positive and negative areas in physics
NEXT STEPS
- Study the concept of area under the curve in integration
- Learn how to differentiate between positive and negative areas in physics
- Explore integration of piecewise functions for varying acceleration
- Review the relationship between acceleration, velocity, and displacement
USEFUL FOR
Students studying physics or calculus, particularly those focusing on kinematics and integration techniques, as well as educators looking for examples of real-world applications of these concepts.