MHB Find Work to Empty Conical Frustum Tank - Juan's Question at Yahoo Answers

[MarkFL]

Here is the question:

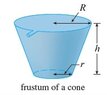
A tank is full of water. Find the work required to pump the water out of the spout. Use the fact that water...?

A tank is full of water. Find the work required to pump the water out of the spout. Use the fact that water weighs 62.5 lb/ft3. (Assume r = 6 ft, R = 12 ft, and h = 24 ft.)

*Picture*

View attachment 1237

___ft-lb___6.4, 5

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Juan,

Let's orient a vertical $y$-axis coinciding with the axis of symmetry of the tank, with the origin at the top surface and the positive direction is down. Let us the decompose the tank into horizontal circular slices, where the radius of each slice decreases linearly as $y$ increases. We may let $r_y$ denote the radius of an arbitrary slice.

We know:

$$r_y(0)=R,\,r_y(h)=r$$

Hence:

$$r_y(y)=\frac{r-R}{h}y+R$$

And so the volume of the arbitrary slice is:

$$dV=\pi\left(\frac{r-R}{h}y+R \right)^2\,dy$$

Now, the weight $w$ of this slice can be found from the fact that weight is mass times the acceleration due to gravity, and mass is mass density $\rho$ times volume. Thus:

$$w=mg=g\rho dV=\pi g\rho\left(\frac{r-R}{h}y+R \right)^2\,dy$$

Now, the work done to lift this slice to the top of the tank is:

$$dW=Fd$$

Where the applied force $F$ is the weight of the slice, and the distance over which this force is applied is $y$. And so we have:

$$dW=\pi g\rho y\left(\frac{r-R}{h}y+R \right)^2\,dy$$

Expanding the square, and distributing the $y$, we have:

$$dW=\pi g\rho\left(\left(\frac{r-R}{h} \right)^2y^3+\frac{2R(r-R)}{h}y^2+R^2y \right)\,dy$$

Summing up all the work elements by integrating, we obtain:

$$W=\pi g\rho\int_0^h \left(\frac{r-R}{h} \right)^2y^3+\frac{2R(r-R)}{h}y^2+R^2y\,dy$$

$$W=\pi g\rho\left[\left(\frac{r-R}{2h} \right)^2y^4+\frac{2R(r-R)}{3h}y^3+\frac{R^2}{2}y^2 \right]_0^h=\pi g\rho\left(\left(\frac{r-R}{2h} \right)^2h^4+\frac{2R(r-R)}{3h}h^3+\frac{R^2}{2}h^2 \right)$$

$$W=\pi g\rho h^2\left(\left(\frac{r-R}{2} \right)^2+\frac{2R(r-R)}{3}+\frac{R^2}{2} \right)=\frac{\pi g\rho h^2}{12}\left(3r^2+2rR+R^2 \right)$$

Using the given data:

$$g\rho=62.5\frac{\text{lb}}{\text{ft}^3},\,h=24 \text{ ft},\,r=6\text{ ft},\,R=12\text{ ft}$$

we find:

$$W=\frac{\pi\left(62.5\frac{\text{lb}}{\text{ft}^3} \right)\left(24\text{ ft} \right)^2}{12}\left(3\left(6\text{ ft} \right)^2+2\left(6\text{ ft} \right)\left(12\text{ ft} \right)+\left(12\text{ ft} \right)^2 \right)=1188000\pi\text{ ft}\cdot\text{lb}$$