Mathematica Finding a function to best fit a curve

Click For Summary
To fit the specified curve, which exhibits a slow decline followed by a rapid rise, a suitable approach is to consider functions resembling an upside-down resonance curve. This type of curve can often be modeled using functions related to low-pass filters. Exploring a logarithmic scale for the ordinate may also enhance the fitting process, potentially providing a clearer representation of the curve's behavior. Resources such as instructional videos on low-pass filter resonance curves can offer additional insights into suitable fitting techniques.
kelly0303
Messages
573
Reaction score
33
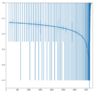
Hello! I want to fit a function to the curve I attached (the first image shows the full curve, while the second one is a zoom-in in the final region). Please ignore the vertical lines, what I care about is the main, central curve. It basically goes down slowly and then it has a fast rise. What is the best function that I can try to use to fit this kind of curve? Thank you!
 

Attachments

  • Screen Shot 2019-11-29 at 04.06.25.png
    Screen Shot 2019-11-29 at 04.06.25.png
    15.3 KB · Views: 329
  • Screen Shot 2019-11-29 at 03.59.27.png
    Screen Shot 2019-11-29 at 03.59.27.png
    14.2 KB · Views: 315
Physics news on Phys.org
What is it ?

Looks like an upside down resonance curve like

1575024971485.png
(from here)

Also: googling 'low-pass filter resonance curve' yields this nice video.

Perhaps you can try a log scale for the ordinate ?
 

Similar threads

Mathematica Fitting solution function of NDSolve with a curve
  • · Replies 1 ·
Replies
1
Views
1K
Integral curve fitting in origin
  • · Replies 8 ·
Replies
8
Views
3K
Mathematica Extract points from an interpolated curve (not a function)
  • · Replies 4 ·
Replies
4
Views
2K
MATLAB Weighting data points with fitted curve in Matlab
  • · Replies 6 ·
Replies
6
Views
5K
MATLAB Troubleshooting Best Fit Line and Distance Calculation in MATLAB
  • · Replies 14 ·
Replies
14
Views
3K
MATLAB Forcing the best fit line to pass through a certain point (Octave)
  • · Replies 12 ·
Replies
12
Views
7K
Press fit curve analysis of two different bushings (force versus displacement)
  • · Replies 7 ·
Replies
7
Views
2K
Undergrad Best fit to an oscillating function
  • · Replies 9 ·
Replies
9
Views
2K
Undergrad Fitting a SiII curve in a supernova spectra
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Finding the Right Curve Fit: A Question About Curve Fitting
  • · Replies 16 ·
Replies
16
Views
3K