codebpr
- 6
- 0
- TL;DR
- I want to plot Hawking temperature as a function of z(inverse of horizon radius), which requires making use of a form factor A(z). I want to make an ansatz for form factor such that I get the desired plots.
This is basically a physics problem but I will try my best to highlight the mathematics behind it.
Suppose I have two functions:
$$T(z,B)=\frac{\text{z}^3 e^{-3 A(\text{z})-B^2 \text{z}^2}}{4 \pi \int_0^{\text{z}} \xi ^3 e^{-3 A(\xi )-B^2 \xi ^2} \, d\xi },$$
$$\phi(z,B)=\int_0^z \sqrt{-\frac{2 \left(3 x A''(x)-3 x A'(x)^2+6 A'(x)+2 B^4 x^3+2 B^2 x\right)}{x}} \, dx$$ where z \in \mathbb{R^+} and B \in [0,1]
and I want to find a function A(z), which is known as the form factor in literature, such that the plot of the function T(z,B) v/s z has one local minimum along with the condition that T(z,B)\rightarrow\infty when z\rightarrow0, also \phi(z) is real-valued. When I take the ansatz A(z)=-a z^2, I am able to satisfy the above condition for B\in[0,0.6] and get plots like:
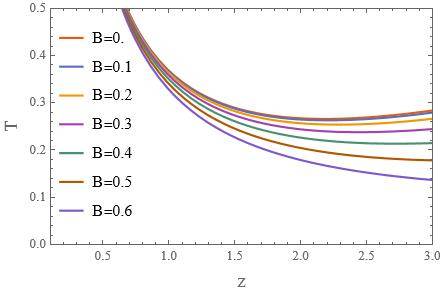
Now for a different model, I need to use such an ansatz for A(z) such that I may be able to satisfy the real valued-ness of \phi(z) and get a local minimum as well as a maximum for the plot of T(z,B) v/s z with the condition that T(z,B)\rightarrow\infty when z\rightarrow0 and T(z,B)\rightarrow0 when z\rightarrow\infty to get plots like these:
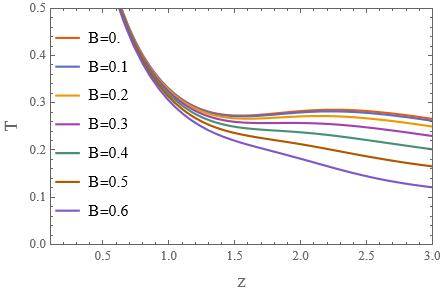
If possible I want to keep B\in[0,1]. The constant a has to be used in the form factor somehow, whose value is 0.15. The form factor can also be written in terms of A(z,B). Is there a way to use Mathematical analysis to come up with such a form factor? Any help in this regard would be truly beneficial!
Suppose I have two functions:
$$T(z,B)=\frac{\text{z}^3 e^{-3 A(\text{z})-B^2 \text{z}^2}}{4 \pi \int_0^{\text{z}} \xi ^3 e^{-3 A(\xi )-B^2 \xi ^2} \, d\xi },$$
$$\phi(z,B)=\int_0^z \sqrt{-\frac{2 \left(3 x A''(x)-3 x A'(x)^2+6 A'(x)+2 B^4 x^3+2 B^2 x\right)}{x}} \, dx$$ where z \in \mathbb{R^+} and B \in [0,1]
and I want to find a function A(z), which is known as the form factor in literature, such that the plot of the function T(z,B) v/s z has one local minimum along with the condition that T(z,B)\rightarrow\infty when z\rightarrow0, also \phi(z) is real-valued. When I take the ansatz A(z)=-a z^2, I am able to satisfy the above condition for B\in[0,0.6] and get plots like:
Now for a different model, I need to use such an ansatz for A(z) such that I may be able to satisfy the real valued-ness of \phi(z) and get a local minimum as well as a maximum for the plot of T(z,B) v/s z with the condition that T(z,B)\rightarrow\infty when z\rightarrow0 and T(z,B)\rightarrow0 when z\rightarrow\infty to get plots like these:
If possible I want to keep B\in[0,1]. The constant a has to be used in the form factor somehow, whose value is 0.15. The form factor can also be written in terms of A(z,B). Is there a way to use Mathematical analysis to come up with such a form factor? Any help in this regard would be truly beneficial!
Last edited: