Finding amplitude and wave speed in a sinusoidal wave.

[Taniaz]

Homework Statement

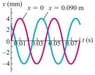
A sinusoidal wave is propagating along a stretched string that lies along the x-axis. The displacement of the string as a function of time is graphed in the figure (attachment) for particles at x=0m and x=0.0900m.
(A) What is the amplitude of the wave?
4mm
(B) What is the period of the wave?
0.04s
(C) You are told that the two points x=0 an x=0.09m are within one wavelength of each other. If the wave is moving in the +x-direction, determine the wavelength and wave speed.
ANSWER KEY: 0.14m and 3.5m/s

I am confused about this part:

(D) If the wave is moving in the -x-direction, determine the wavelength and wave speed.
ANSWER KEY: 0.24m and 6.0m/s

(e) Would it be possible to determine definitively the wavelength in parts (c) and (d) if you were not told that the two points were within one wavelength of each other? Why or why not?
NO

Homework Equations

y(x,t)=Acos(kx +/- ωt)
v=λf

The Attempt at a Solution

Apparently, for part d, they did 0.09 m / 0.015 s to get the velocity and I'm not sure how they got 0.015s for the time when it's moving in the negative x-direction. You get this time if the peak of x=0 shifts to t=0.05 s because it's traveling in the opposite direction so the peak of x=0 comes before x = 0.09, and then you do 0.05-0.035 to get this? Is this right?

 

[BvU]

You get this time if the peak of x=0 shifts to t=0.05 s because it's traveling in the opposite direction so the peak of x=0 comes before x = 0.09, and then you do 0.05-0.035 to get this? Is this right?

is a bit confusing to me.

Back to part c: (for which I miss your solution ?) I prefer to express it as $\ \ y_{0.09}(t+0.25) = y_0(t)$ (*) so you have to wait 0.25 sec before the y at x=0 reaches x=0.09 for the case of a wave moving in the +x direction.

(*) of course 0.65 etc also satisfy, but we are given that $\delta x < \lambda$With this approach it might also be easier to tackle part d)

 

[Taniaz]

For c, I basically took the time between the 2 peaks and that was 0.035-0.01=0.025
Then 0.09/0.025 = 3.6 m/s and then use v=λf for the wavelength.

For d, because it's traveling in the negative x-direction so the peak at x=0 would actually come before x=0.09

 

[BvU]

It seems that for c) you intuitively took the 'time between the two peaks' going in the correct direction, namely from 0.035 to 0.01. (I always have to force myself to think long and hard about which direction).

And then for d) it's " the other 'time between the two peaks' " .

In short: you did it right

 

[Taniaz]

Great! Thank you!