tdoyzz
- 8
- 0
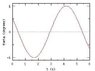
1. What is the amplitude of the pendulum's motion, in meters? (see attached graph)
Given: angular frequency=1.26rad/s
2. T=2pi(L/g)^.5; a=-w^2(x); s(t)=Acos(wt+phase); theta=s/L
3. I almost don't even know how to start.. The confusing part I believe is the graph. The max angle says its 1.. so I solve for L and got 6.19m, with the period being 5s. But I still keep getting wrong answers. Please help. Thanks
Given: angular frequency=1.26rad/s
2. T=2pi(L/g)^.5; a=-w^2(x); s(t)=Acos(wt+phase); theta=s/L
3. I almost don't even know how to start.. The confusing part I believe is the graph. The max angle says its 1.. so I solve for L and got 6.19m, with the period being 5s. But I still keep getting wrong answers. Please help. Thanks