SUMMARY
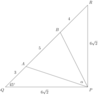
The discussion focuses on finding the angle $\angle APB$ in triangle $PQR$, where $\angle P=90^{\circ}$ and $PQ=PR$. Given the segment ratios $QA:AB:BR=3:5:4$, the calculations reveal that if $QA=3$, $AB=5$, and $BQ=4$, the sides of triangle $PQR$ measure $6\sqrt{2}$ units. Using the cosine rule, it is determined that $\angle APB = 45^\circ$.
PREREQUISITES
- Understanding of triangle properties, specifically right triangles.
- Familiarity with the cosine rule in trigonometry.
- Knowledge of segment ratios and their implications in geometric constructions.
- Ability to perform calculations involving square roots and trigonometric functions.
NEXT STEPS
- Study the cosine rule in-depth, particularly its applications in various triangle types.
- Explore geometric properties of right triangles, focusing on isosceles right triangles.
- Investigate segment division ratios and their effects on triangle geometry.
- Practice solving similar problems involving angle calculations in triangles with given segment ratios.
USEFUL FOR
Mathematicians, geometry enthusiasts, and students studying trigonometry or preparing for competitive exams will benefit from this discussion.