SUMMARY
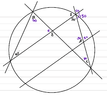
The discussion centers on determining the angle at $\gamma$ using the vertical angles theorem. The user initially struggles to identify the correct theorem but ultimately confirms that $\gamma$ represents the angle formed by two intersecting lines. The clarification that $\gamma$ is indeed an angle between these lines simplifies the problem, leading to a resolution with the application of the vertical angles theorem.
PREREQUISITES
- Understanding of basic geometric concepts, specifically angles and lines.
- Familiarity with the vertical angles theorem.
- Knowledge of circle geometry and angle relationships.
- Ability to visualize geometric figures and their properties.
NEXT STEPS
- Study the properties of vertical angles in more depth.
- Explore the relationship between angles formed by intersecting lines and circles.
- Learn about other relevant theorems in circle geometry, such as the inscribed angle theorem.
- Practice solving problems involving angles and their relationships in various geometric configurations.
USEFUL FOR
Students studying geometry, educators teaching geometric principles, and anyone seeking to enhance their understanding of angle relationships in geometric figures.