Finding $b(a+c)$ Given Roots of a Cubic Equation

[anemone]

let $a>b>c$ be roots of $\sqrt{2015}x^3-4031x^2+2=0$, find $ b(a+c)$.

 

[kaliprasad]

let $a>b>c$ be roots of $\sqrt{2015}x^3-4031x^2+2=0$, find $ b(a+c)$.

Spoiler

to avoid surds let $t=\sqrt{2015}$so we get $tx^3 - (2t^2+1)x^2 + 2 = 0$
or $tx^3 - x^2 - 2t^2x^2+2=0$
or $x^2(xt-1) - 2(x^2t^2-1) = 0$
or $(x^2(xt-1) - 2 (xt-1)(xt+1) = 0$
so xt = 1 or $x^2-2xt -2 = 0$

2nd equation gives

$(x-t)^2 = t^2+ 2 = 2017$
so 3 roots are $x=\dfrac{1}{\sqrt{2015}}$ or $x= \sqrt{2015} \pm \sqrt{2017}$clearly $ \sqrt{2015} +\sqrt{2017} \gt \dfrac{1}{\sqrt{2015}} \gt \sqrt{2015} - \sqrt{2017}$so $a= \sqrt{2015} +\sqrt{2017}$
$b = \dfrac{1}{\sqrt{2015}}$
$c = \sqrt{2015} -\sqrt{2017}$

hence b(a+c) = 2

 

[anemone]

Thanks kaliprasad for you good solution!:)

My solution:

Spoiler

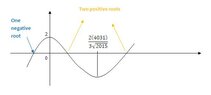
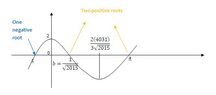
Descartes' Rule of Signs tells us that this cubic polynomial has two positive roots and one negative root, hence, $c$ must be the negative root. . In fact, it has exactly two positive roots and one negative root:

If we let $P(x)=\sqrt{2015}x^3-4031x^2+2$, first and second derivative give us the one maximum and one minimum point that the cubic polynomial possesses, and I label them in the graph below:

$P'(x)=3\sqrt{2015}x^2-2(4031)x=x(3\sqrt{2015}x-2(4031))\rightarrow P'(x)=0\,\,\text{iff}\,\,x=0\,\,\text{or}\,\,x=\dfrac{2(4031)}{3\sqrt{2015}}$

$P''(x)=2(3\sqrt{2015}x)-2(4031)\rightarrow P''(0)=\text{-ve}\,\,\text{and}\,\,P''(\dfrac{2(4031)}{3\sqrt{2015}})=\text{+ve}$

View attachment 3890

Now, if we let $b,\,(a+c)$ be the roots of a quadratic polynomials, we see that we can have

$x^2-(b+a+c)x+b(a+c)=0$

$x^2-\left(\dfrac{4031}{\sqrt{2015}}\right)x+b(a+c)=0$

Replace $b$ in the equation above and then multiplying it with $b\sqrt{2015}$, we get

$\sqrt{2015}b^3-4031b^2+b(a+c)(b\sqrt{2015})=0$

$\therefore (-2)+b(a+c)(b\sqrt{2015})=0$

$b(a+c)=\dfrac{2}{b\sqrt{2015}}$

It's now tempting to check if $b=\dfrac{1}{\sqrt{2015}}$ is a root for the given cubic polynomial:

$P(\dfrac{1}{\sqrt{2015}})=\sqrt{2015}\left(\dfrac{1}{\sqrt{2015}}\right)^3-4031\left(\dfrac{1}{\sqrt{2015}}\right)^2+2=0$

View attachment 3891

and therefore, out intuition is right and that $b(a+c)=\dfrac{2}{b\sqrt{2015}}=\dfrac{2}{\left(\dfrac{1}{\sqrt{2015}}\right)\sqrt{2015}}=2$

 

[kaliprasad]

Thanks kaliprasad for you good solution!:)

My solution:

Spoiler

Descartes' Rule of Signs tells us that this cubic polynomial has two positive roots and one negative root, hence, $c$ must be the negative root. . In fact, it has exactly three positive roots:

Spoiler

why the incorrect statement In fact, it has exactly three positive roots:

 

[anemone]

Spoiler

why the incorrect statement In fact, it has exactly three positive roots:

Hi kaliprasad, isn't $\sqrt{2015}-\sqrt{2017}<0$ ?(Wink)

 

[Greg]

Spoiler

$$f(x)=\sqrt{2015}x^3-4031x^2+2=0\implies x^3-\frac{4031}{\sqrt{2015}}x^2+\frac{2}{\sqrt{2015}}=0$$

By inspection, one of the roots is

$$\frac{1}{\sqrt{2015}}$$

(I must admit here that I looked at the other solutions before I came up with this).

$$f'(x)=3\sqrt{2015}x^2-8062x$$

The above is negative at $$x=\frac{1}{\sqrt{2015}}$$, so we may conclude that all three roots are real and that $$b=\frac{1}{\sqrt{2015}}$$.

From Vieta's formulae,

$$abc=\frac{-2}{\sqrt{2015}}\implies ac=-2$$

and

$$ab+ac+bc=0\implies b(a+c)=-ac=2$$

as required.

 

[kaliprasad]

Hi kaliprasad, isn't $\sqrt{2015}-\sqrt{2017}<0$ ?(Wink)

sorry for misunderstanding

Spoiler

In fact, it has exactly three positive roots:

this statement is yours and not mine and I wanted to ask why this statement.This statement should not be there. (post 3 your statement)

 

[anemone]

$$f(x)=\sqrt{2015}x^3-4031x^2+2=0\implies x^3-\frac{4031}{\sqrt{2015}}x^2+\frac{2}{\sqrt{2015}}=0$$

By inspection, one of the roots is

$$\frac{1}{\sqrt{2015}}$$

(I must admit here that I looked at the other solutions before I came up with this).

$$f'(x)=3\sqrt{2015}x^2-8062x$$

The above is negative at $$x=\frac{1}{\sqrt{2015}}$$, so we may conclude that all three roots are real and that $$b=\frac{1}{\sqrt{2015}}$$.

From Vieta's formulae,

$$abc=\frac{-2}{\sqrt{2015}}\implies ac=-2$$

and

$$ab+ac+bc=0\implies b(a+c)=-ac=2$$

as required.

Excellent, greg1313! And thanks for participating!:)

 

[anemone]

sorry for misunderstanding

Spoiler

In fact, it has exactly three positive roots:

this statement is yours and not mine and I wanted to ask why this statement.This statement should not be there. (post 3 your statement)

Ah! I see...yes, I re-read post #3 and you are right, I said the given cubic polynomial has exactly three positive roots when it has 2 positive and 1 negative roots, I don't know where my head was when I said that, hehehe...sorry!

I will fix that third post and thanks for catching, Kali!

 

[kaliprasad]

Ah! I see...yes, I re-read post #3 and you are right, I said the given cubic polynomial has exactly three positive roots when it has 2 positive and 1 negative roots, I don't know where my head was when I said that, hehehe...sorry!

I will fix that third post and thanks for catching, Kali!

Spoiler

your head was , is and will be where it should be. On top of your shoulders.