- #1
freshcoast
- 185
- 1
1. Problem statement.
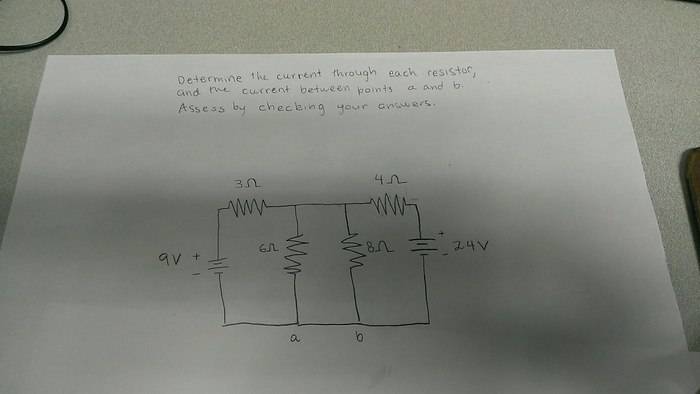
2. Known equations
Kirchoffs law, logic
3. Attempt
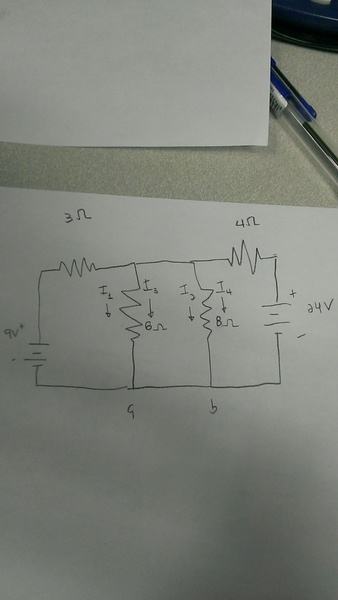
I believe there are 4 currents, as shown above. i1 and i2 are coming from the 9 volt battery in a clockwise direction and i3 and i4 are from the 24v battery in a anti clockwise direction. I just apply kirchkoffs law for each current with the resistor in its path way.
Ex. For i1 the equation would look like
9v - i1(3ohms) -i1(6ohms) = 0
Then
A = i1 + i3
B = i2 + i4
2. Known equations
Kirchoffs law, logic
3. Attempt
I believe there are 4 currents, as shown above. i1 and i2 are coming from the 9 volt battery in a clockwise direction and i3 and i4 are from the 24v battery in a anti clockwise direction. I just apply kirchkoffs law for each current with the resistor in its path way.
Ex. For i1 the equation would look like
9v - i1(3ohms) -i1(6ohms) = 0
Then
A = i1 + i3
B = i2 + i4
 Point a is a dot marked on a schematic. I2 is a current and it has units of amperes.
Point a is a dot marked on a schematic. I2 is a current and it has units of amperes.